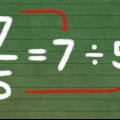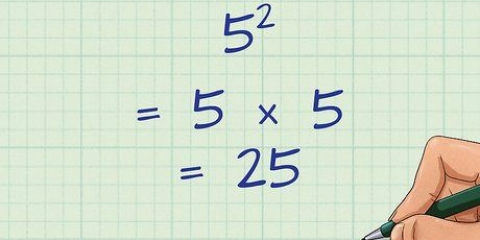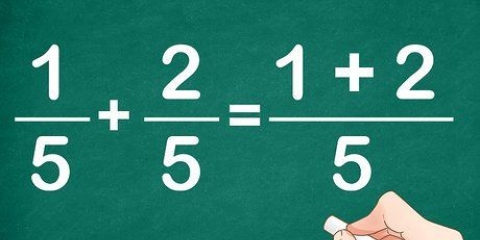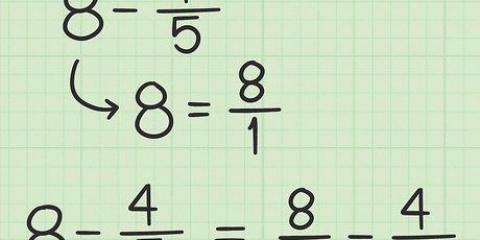Por ejemplo, tomemos 4/8 de nuevo. Si, en lugar de multiplicar, dividimos el numerador y el denominador por 2, obtenemos (4 2)/(8 ÷ 2) = 2/4. 2 y 4 son números enteros, por lo que esta fracción equivalente es válida. 
El máximo común divisor (GGD) del numerador y el denominador es el número entero más grande por el cual tanto el numerador como el denominador son divisibles. Entonces, en nuestro ejemplo 4/8, porque 4 es el mayor divisor de 4 y 8, dividimos el numerador y el denominador de nuestra fracción por 4 para obtener los términos más simples. (4 4)/(8 ÷ 4) = 1/2. 
Para convertir una fracción impropia, multiplica el entero del número mixto por el denominador de la fracción, luego suma el producto al numerador. Por ejemplo, 1 2/3 = ((1 × 3) + 2)/3 = 5/3. Luego puede convertirlo nuevamente si es necesario. Por ejemplo, 5/3 × 2/2 = 10/6, sigue siendo el mismo que 1 2/3. Sin embargo, no es necesario convertir una fracción impropia. Podemos ignorar el entero y simplemente convertir la fracción y luego agregarle el entero. Por ejemplo, en 3 4/16, solo estamos viendo 4/16. 4/16 ÷ 4/4 = 1/4. Así que ahora volvemos a sumar el entero y obtenemos un nuevo número mixto, 3 1/4. Por ejemplo, arriba encontramos que 4/8 ÷ 4/4 = 1/2 . Si añadiéramos 4/4 a esto, habríamos obtenido una respuesta completamente diferente. 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 o 3/2, y ninguno de estos es igual a 4/8. Por ejemplo, supongamos que tenemos la ecuación ((x + 3)/2) = ((x + 1)/4). En este caso, lo resolvemos por multiplicación cruzada: (x + 3) × 4 = 4x + 12 (x + 1) × 2 = 2x + 2 2x + 2 = 4x + 12 2 = 2x + 12 -10 = 2x -5 = x Por ejemplo, tomamos la ecuación ((x +1)/3) = (4/(2x - 2)). Primera multiplicación cruzada: (x + 1) × (2x - 2) = 2x + 2x -2x - 2 = 2x - 2 4×3 = 12 2x - 2 = 12. En este punto, queremos convertir esto en una ecuación cuadrática (ax + bx + c = 0) restando 12 de ambos lados, dando 2x - 14 = 0. Ahora usamos la fórmula (x = (-b +/- √(b - 4ac))/2a) para encontrar el valor de x: x = (-b +/- √(b - 4ac))/2a. En nuestra ecuación, 2x - 14 = 0, a = 2, b = 0 y c = -14. x = (-0 +/- √(0 - 4(2)(-14))))/2(2) x = (+/- √( 0 - -112))/2(2) x = (+/- √(112))/2(2) x = (+/- 10.58/4) x = +/- 2.64 En este punto, comprobamos nuestra respuesta sustituyendo 2,64 y -2,64 en la ecuación cuadrática original.
Resolver fracciones equivalentes
Contenido
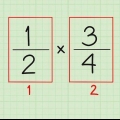
dos fracciones son "equivalente" si tienen el mismo valor. Por ejemplo, las fracciones 1/2 y 2/4 son equivalentes porque 1 sobre 2 tiene el mismo valor que 2 sobre 4 (0,5 en forma decimal). Saber cómo convertir una fracción a otra fracción equivalente es un valor matemático esencial que necesita, desde álgebra básica hasta matemáticas avanzadas. Mire el Paso 1 para comenzar!
Pasos
Método 1 de 2: crear fracciones equivalentes

1. Multiplica el numerador y el denominador de una fracción por el mismo número para obtener una fracción equivalente. Dos fracciones que son diferentes pero tienen equivalente por definición, numeradores y denominadores que son múltiplos entre sí. En otras palabras, multiplicar el numerador y el denominador de una fracción por el mismo número producirá una fracción equivalente. Aunque los números en esta nueva fracción son diferentes, todavía tiene el mismo valor.
- Por ejemplo, si tomamos la fracción 4/8 y multiplicamos el numerador y el denominador por 2, obtenemos (4×2)/(8×2) = 8/16. Estas dos fracciones son equivalentes.
- (4 × 2)/(8 × 2) es esencialmente lo mismo que 4/8 × 2/2. Recuerda que cuando multiplicamos dos fracciones lo hacemos así: numerador por numerador y denominador por denominador. Tenga en cuenta que 2/2 es igual a 1. Entonces es fácil ver por qué 4/8 es igual a 8/16: la segunda fracción es la primera fracción multiplicada por 2!
2. Divide el numerador y el denominador o una fracción por el mismo número para obtener una fracción equivalente. Al igual que la multiplicación, la división también se puede usar para crear una nueva fracción equivalente a la fracción dada. Simplemente divide el numerador y el denominador de una fracción por el mismo número para obtener una fracción equivalente. Aquí hay una advertencia: la fracción resultante debe consistir en números enteros tanto en el numerador como en el denominador para que sea válida.

3. Simplifica tu fracción usando el máximo común divisor (GGD). Cualquier fracción dada tiene un número infinito de fracciones equivalentes: puedes multiplicar el numerador y el denominador por cualquier número entero, grande o pequeño para obtener una fracción equivalente. Pero la forma más simple de una fracción dada suele ser la que tiene los términos más pequeños. En ese caso, el numerador y el denominador son lo más pequeños posible; ya no se pueden dividir por ningún número entero para que el término sea aún más pequeño. Para simplificar una fracción, dividimos el numerador y el denominador por el máximo común divisor.

4. Si lo desea, convierta números mixtos en fracciones impropias para facilitar la conversión. Por supuesto, no todas las fracciones que encuentres serán tan fáciles de simplificar como 4/8. Por ejemplo, números mixtos (p. ej. 1 3/4, 2 5/8, 5 2/3, etc.) puede hacer que esta conversión sea un poco más difícil. Si desea hacer una fracción de un número mixto, puede hacerlo de dos maneras: convierta el número mixto en una fracción impropia y luego continúe, o mantener el número mixto y dar un número mixto como respuesta.
5. Nunca sume o reste para obtener fracciones equivalentes. Al convertir fracciones a su forma equivalente, es importante recordar que las únicas operaciones que aplica son la multiplicación y la división. Nunca use sumas o restas. La multiplicación y la división funcionan para obtener fracciones equivalentes porque estas operaciones son en realidad formas del número 1 (2/2, 3/3, etc.).) y dé respuestas que sean iguales a la fracción con la que comenzó. La suma y la resta no tienen esta capacidad.
Método 2 de 2: resolver fracciones equivalentes con variables
1. Usar la multiplicación cruzada para resolver problemas de equivalencia de fracciones. Un tipo complicado de problema de álgebra que trata con fracciones equivalentes involucra ecuaciones con dos fracciones, donde una o ambas contienen una variable. En casos como este, sabemos que estas fracciones son equivalentes porque son los únicos términos a ambos lados del signo igual de una ecuación, pero no siempre es obvio cómo resolver la variable. Afortunadamente, podemos multiplicar por en cruz, resolver este tipo de problemas sin ningún problema.
- La multiplicación cruzada es exactamente lo que parece: estás multiplicando de manera cruzada sobre el signo igual. En otras palabras, multiplicas el numerador de una fracción por el denominador de la otra fracción y viceversa. Luego resuelves la ecuación más.
- Por ejemplo, tenemos la ecuación 2/x = 10/13. Ahora multiplique en cruz: multiplique 2 por 13 y 10 por x, y resuelva más la ecuación:
- 2×13 = 26
- 10 × x = 10 x
- 10x = 26. Ahora resolvemos la ecuación más. x = 26/10 = 2.6
2. Use la multiplicación cruzada de la misma manera que las ecuaciones multivariadas o las expresiones variables. Una de las mejores características de la multiplicación cruzada es que funciona prácticamente igual ya sea que estés tratando con dos fracciones simples o complejas. Por ejemplo, si ambas fracciones contienen variables, entonces nada cambiará; solo tendrás que deshacerte de estas variables. Del mismo modo, si los numeradores o denominadores de su variable de fracción contienen expresiones, simplemente "seguir multiplicándose" usando la propiedad distributiva y resolviendo como lo haces normalmente.
3. Usar técnicas para resolver polinomios. La multiplicación cruzada no funciona siempre un resultado que puedes resolver con álgebra simple. Si está tratando con términos variables, obtendrá rápidamente como resultado una ecuación cuadrática u otro polinomio. En tales casos se utiliza, por ejemplo, el cuadrado y/o la fórmula del cuadrado.
Consejos
- Convertir fracciones a una forma equivalente es en realidad como multiplicar por una fracción como 2/2 o 5/5. Dado que esto es en última instancia igual a 1, el valor de la fracción permanece igual.
Advertencias
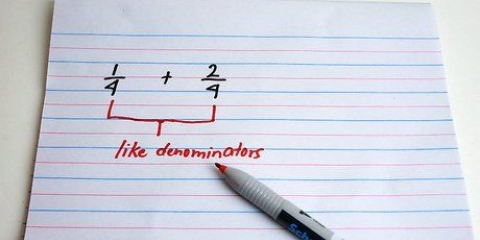
- Sumar y restar fracciones es diferente a multiplicar y dividir fracciones.
Artículos sobre el tema. "Resolver fracciones equivalentes"
Оцените, пожалуйста статью
Popular