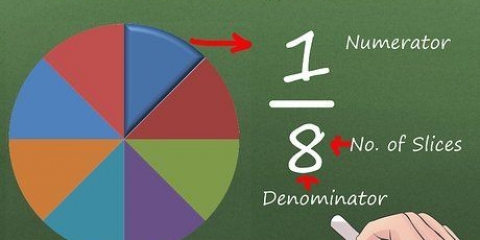
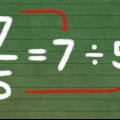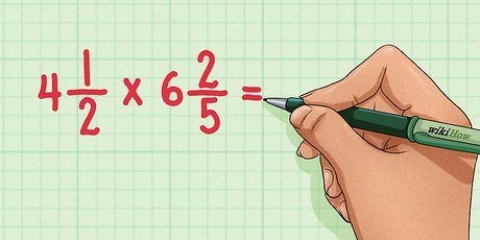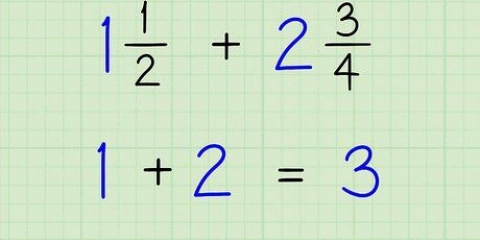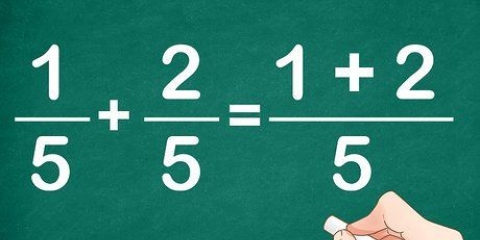= 

Ejemplo: reescribir  como un numero mixto.
como un numero mixto. ¿Cuántas veces cabe exactamente 5 en 36?? 5x 7 = 35; , entonces el entero del número mixto es 7. ¿Qué nos queda ahora?? La parte entera es equivalente a  , así que adelante
, así que adelante  -
-  =
= 
Combina el entero y la fracción:  =
= 


Ejemplo: 















Restar fracciones de números enteros
Contenido
Restar fracciones de números enteros no es tan difícil como parece. Las dos formas principales de hacer esto son: convertir el número entero en una fracción, o restar 1 del número entero y convertir ese 1 en una fracción con el mismo denominador que la fracción que estás restando. Una vez que tenga fracciones con el mismo denominador, puede comenzar con la suma menos. Ambos métodos te permitirán restar fracciones de números enteros rápida y fácilmente.
Pasos
Método 1 de 2: Resta fracciones de números enteros

1. Convertir el número entero a una fracción. Haces esto dando al número entero un denominador de 1.
- Ejemplo:

2. Convertir dos fracciones con denominadores comunes. El denominador de la fracción original es también el mínimo común denominador (LCD) de estas dos fracciones. Multiplica el numerador y el denominador del entero del que hiciste una fracción por este número para que ambas fracciones tengan el mismo denominador.




3. Restar los numeradores. Ahora que ambas fracciones tienen el mismo denominador, puedes restar los denominadores entre sí como una suma regular menos:




4. Convertir a un número mixto (opcional). Si su respuesta es una fracción impropia, es posible que deba reescribirla como un número mixto:
 como un numero mixto.
como un numero mixto. , así que adelante
, así que adelante  -
-  =
= 
 =
= 
Método 2 de 2: método alternativo

1. Prueba esto para números enteros más grandes. ¿Viste cómo el método anterior convierte un número entero en una fracción y finalmente lo vuelve a convertir en un número mixto?? Este método te permite saltarte parte de este método para que la fracción se resuelva con números pequeños.

2. Convertir una fracción impropia a un número mixto. Salta este paso si tu fracción no es impropia. (En una fracción impropia, el numerador es mayor que el denominador).




3. Divide el número entero en un 1 y otro número entero. Por ejemplo: reescribe 5 como 4 + 1, o 22 como 21 + 1.



4. Convertir el 1 a una fracción. En este punto, usamos el método anterior para resolver esa parte del problema en forma de "1 - (fracción)". El otro entero permanece sin cambios para el resto de las soluciones.



5. Multiplica para dar a ambas fracciones el mismo denominador. Como se indicó anteriormente, multiplique el numerador y el denominador por el mismo número para que la fracción convertida tenga el mismo denominador que el original.



6. Resta ambas fracciones entre sí. Resta los numeradores de ambas fracciones para resolver la parte fraccionaria de la ecuación.



Artículos de primera necesidad
- Lápiz
- Papel
Artículos sobre el tema. "Restar fracciones de números enteros"
Оцените, пожалуйста статью
Popular