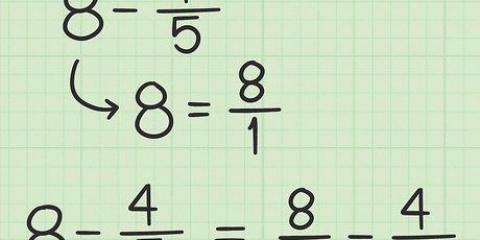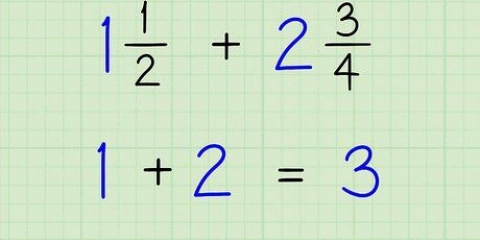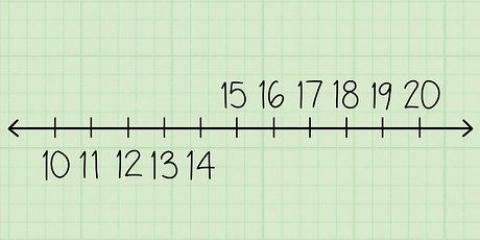Su libro de matemáticas podría llamar a este punto punto de origen, porque este es el punto donde los números de surge, o empezar. 
No se preocupe demasiado por el espaciado perfecto: siempre que lo parezca, la recta numérica funcionará bien. 
El ejemplo es una línea numerada de -6 a 6. 
Las fracciones como 1/2 son parte de un número, no números enteros. Del mismo modo con un decimal como 0,25; los decimales no son enteros. 
¿Encuentras esto un poco demasiado fácil?? No te resultará extraño sumar y podrás resolver 1 + 2 de memoria. Genial: si ya sabes la respuesta, es más fácil entender cómo funciona la recta numérica. Luego, puede comenzar a usar una recta numérica para problemas más complicados o para prepararse para matemáticas y álgebra. 




Como ejemplo tomamos la suma 1 + -4. En una recta numérica comenzamos en 1, nos movemos 4 espacios a la izquierda y terminamos en -3. 

Como ejemplo, tome -4. Si sumas -4 a 1, reduce 1 en 4. O de forma matemática:
1 + (-4) = 1 - 4
Escribimos esto en una recta numérica, y colocamos nuestro dedo en el 1, luego te mueves 4 espacios a la izquierda (en otras palabras, sumas con -4). Dado que es una ecuación, la izquierda es igual a la derecha, por lo que también se cumple lo contrario:
1 - 4 = 1 + (-4)

En una recta numérica comenzamos en 5, disminuimos en 8 y terminamos en -3. Esto se nota como
5 - 8 = -3



Ya sabemos que 5 - 8 = -3, así que omitamos 5 - 8 de nuestra ecuación y pongamos -3 en ella:
5 - (8 - 1) = 5 - 7 = -3 + 1
Ya sabemos lo que es 5 - (8 - 1): mueves un marcador menos de 5 - 8. Nuestra ecuación muestra que 5 - 8 = -3, y 1 paso menos es -2. Ahora nuestra ecuación se puede escribir como:
-3 - (-1) = -3 + 1



Debajo de los dos números a la derecha, 3 y 1, anota la respuesta de la suma de ambos números: 4 Entonces. 
La respuesta que obtienes es, si lo hiciste bien: 9964. Si cometiste un error, comprueba tu efecto. 

Si quieres saber cómo funciona esto, piensa en lo que significa dividir el 1 y el 2. En realidad divides 12 en 10 y 2. Puede escribir el 10 arriba de los números si lo desea, después de lo cual notará que el 1 se alinea con el 5 y el 3, como debería. 

Puedes intentar problemas un poco más difíciles, como 974+568. Recuerda que cada vez que obtienes un número de dos dígitos, solo colocas el último dígito con la respuesta y el primer dígito arriba del siguiente par de números (la siguiente columna). Si la última suma tiene una respuesta de dos dígitos, puede colocar ambos en la respuesta debajo de la línea. Mire los Consejos para obtener una respuesta al problema 974+568 para verificar su propia respuesta. 

La respuesta debería ser: 4211. 

Tacha el 2 del número de arriba y escribe un 1. allí. El 2 está directamente a la izquierda del 4. Tacha el 4 y hazlo 14. Haga esto en un espacio pequeño, para que quede claro a qué par de números pertenece 14, y así indica 14 – 8. También puede escribir un 1 antes del 4, si hay suficiente espacio. Lo que acabas de hacer es "a prestar" de un 1 de la columna con decenas, o también la segunda columna de la derecha, para que puedas sumar 10 a 4. Esto le dará 14 en la columna con unidades. 

Tu respuesta hasta ahora pertenece 06 ser - estar. 

Asegúrese de que los números sean correctos antes de compararlos. 912 es no mayor que 5000, que es fácil de ver si los números están alineados correctamente, porque el 5 no está por encima de nada. Puedes poner 1 o más ceros antes del número, si eso ayuda. Por ejemplo, escriba 912 como 0912 para que tenga la misma longitud que 5000. 

El nuevo problema a resolver es: 968.772 - 415.990 = - ? Mira los Consejos para comprobar tu respuesta. 

Supongamos que tienes 4 + -7. Haga de esto una suma menos: 4 - 7 Invierte el orden y haz que la suma sea negativa: -(7 – 4) = -(3) = -3. Si no está acostumbrado a usar paréntesis en sus sumas, piénselo de esta manera: 4 - 7 se convierte en 7 - 4 y agrega un signo menos. Entonces 7 - 4 = 3 y luego haces -3 para obtener la respuesta correcta a la suma 4 - 7. 
-3 + -6 = -9 -15 + -5 = -20 ¿Ves el patrón?? Todo lo que tienes que hacer es sumar los números como si fueran positivos y luego agregarles un signo negativo. -4 + -3 = -(4 + 3) = -7 
Piense en un número negativo como dinero robado. si algo "masturba", o quita del dinero robado para devolverlo, es lo mismo que darle dinero a esa persona, o no? Ejemplo: 10 – -5 = 10 + 5 = 10 Ejemplo: -1 – -2 = -1 + 2. Ya aprendiste cómo resolver esto, en un paso anterior, recuerda? releer "Aprende a sumar un número negativo y uno positivo" si no sabes. Aquí está la solución completa del último ejemplo: -1 – -2 = -1 + 2 = 2 + -1 = 2 – 1 = 1.
Sumar y restar números enteros
Contenido
- Pasos
- Método 1 de 5: suma y resta de números enteros positivos con una recta numérica
- Método 2 de 5: sumar y restar números negativos en una recta numérica
- Método 3 de 5: sumar números enteros positivos grandes
- Método 4 de 5: restar números enteros positivos grandes
- Método 5 de 5: sumar y restar números enteros negativos
- Consejos
lo harías números enteros puede pensar en los números comunes, como 3, -12, 17, 0, 7000 o -582. Los números enteros también se llaman así porque no se dividen en partes de números, como fracciones y decimales. Lea este artículo para aprender todo lo que necesita saber sobre sumar y restar números enteros, o salte directamente a un área con la que necesita ayuda.
Pasos
Método 1 de 5: suma y resta de números enteros positivos con una recta numérica

1. ¿Qué es una recta numérica?. Una recta numérica convierte el trabajo con números en algo real y tangible que puedes imaginar. Usando marcadores y tu mente podemos aplicarlo como una especie de calculadora para sumar y restar números.

2. Dibujar una recta numérica básica. dibujar una línea recta. Coloque una marca en el medio de la línea. Escribe un 0 o cero junto a esta marca.

3. Dibuja dos marcas, 1 a cada lado del cero. escribir -1 junto al marcador de la izquierda y 1 a la derecha. Estos son los enteros más cercanos a cero.

4. Agregar más números a la línea. Coloque más marcadores a la izquierda de -1 y a la derecha de 1. Como sigue: -2, -3, y -4 y a la derecha las marcas 2, 3, y 4, etc. todo lo que puedas poner en el papel.

5. Comprender qué son los números enteros positivos y negativos. Un entero positivo, también llamado número natural, es un entero mayor que cero. 1, 2, 3, 25, 99 y 2007 son números enteros positivos. A negativo entero es un número entero menor que cero (como -2, -4 y -88).

6. Resuelve 1+2 colocando tu dedo en el marcador etiquetado como 1.

7. Haz la suma 1+2 deslizando tu dedo 2 marcas a la derecha. Cuenta el número de marcadores que pasas. ¿Has tenido 2 marcas, para?. El número que señala tu dedo es la respuesta: 3.

8. Otro ejemplo. Supongamos que queremos saber cuánto es 3 + 2. Comience en 3, muévase a la derecha y aumento con 2. terminamos a las 5. Escribes esto como 3 + 2 = 5.

9. Resta números enteros positivos moviéndose hacia la izquierda en la recta numérica. Como ejemplo tenemos la suma 6 – 4. Comenzamos en 6, movemos 4 marcadores a la izquierda y terminamos en 2. Escribes esto como 6 - 4 = 2.
Método 2 de 5: sumar y restar números negativos en una recta numérica

1. Aprende qué es una recta numérica. Si no sabes cómo hacer una recta numérica, vuelve a Sumar y restar números positivos y léelo de nuevo.

2. Entender qué son los números negativos. Los números positivos están del lado derecho del cero y los números negativos del lado izquierdo de la recta numérica. Agregar un número negativo mueve su dedo a izquierda en la recta numérica.

3. Utilizar una comparación para entender sumar con un número negativo. Tenga en cuenta que -3, nuestra respuesta, es la misma si calculamos la suma 1 – 4. 1 + (-4) y 4 - 1 es lo mismo. También podemos escribir esto como un comparación, una forma matemática de mostrar que dos cosas son iguales:
1 + (-4) = 1 - 4 = -3

4. En lugar de sumar un número negativo, también podemos convertirlo en una suma negativa con solo números positivos. Como puede ver en nuestra ecuación simple, podemos ir de dos maneras: "suma un numero negativo" o "restar un número positivo". Es posible que haya tenido que aprender esto sin que le digan por qué: esta es la razón.
Escribimos esto en una recta numérica, y colocamos nuestro dedo en el 1, luego te mueves 4 espacios a la izquierda (en otras palabras, sumas con -4). Dado que es una ecuación, la izquierda es igual a la derecha, por lo que también se cumple lo contrario:

5. Comprender cómo funciona la resta de números negativos en una recta numérica. En una recta numérica, restar un negativo es igual a moverse hacia la derecha. Comencemos con 5 - 8.

6. Reduce el número que restas y mira qué pasa. Supongamos que la suma se convierte en 5 -7. Ahora nos movemos 1 lugar menos a la izquierda en la recta numérica. Escribes esto como
5 - 7 = -2

7. Tenga en cuenta que una disminución puede resultar en un aumento. En este ejemplo, reducimos el número de lugares a la izquierda en 1. Como comparación, esto se convierte en:
5 - 7 = -2 = 5 - (8 - 1)

8. Convierta un menos en un más al sumar números negativos. Usando el paso "cambiar resta a suma", ¿Podemos ahora escribir esto más corto como:
5 - (8 - 1) = 5 - 7 = 5 - 8 + 1 .

9. Escribe la resta de números negativos como una suma. Observe lo que sucedió al final: demostramos que:
-3 + 1 = -3 - (-1)
Podemos expresar esto como una regla matemática simple y más general:
primer número más un segundo número = primer número menos segundo número negativo)
O, en términos más simples como en la clase de matemáticas:
Convierte dos menos en uno más .
Podemos expresar esto como una regla matemática simple y más general:
O, en términos más simples como en la clase de matemáticas:
Método 3 de 5: sumar números enteros positivos grandes

1. Escribe la suma 2503 + 7461 con un número encima del otro. Coloque los números uno encima del otro, de modo que el 2 esté encima del 7, el 5 esté encima del 4, etc. En este método, aprenderemos a sumar números que son demasiado grandes para memorizar o con una recta numérica.
- Escribe un + a la izquierda del número de abajo y una línea debajo.

2. Comience a sumar los dos números en el extremo derecho. Puede parecer extraño empezar por la derecha porque estamos tan acostumbrados a leer los números de izquierda a derecha. Mantenemos este orden porque de lo contrario no obtendremos la respuesta correcta, como verás más adelante.

3. Suma cada número de la misma manera. Trabajando de izquierda a derecha, haga las siguientes adiciones: 0+6, 5+4, y 2+7. Escribe las respuestas debajo de los pares de números.

4. Ahora haz la suma 857+135. Aquí se ve una diferencia con el anterior, porque 7+5 es igual a 12, un número con 2 dígitos. Pero no puedes poner más de 1 dígito debajo de un par de números. Sigue leyendo para saber qué hacer y por qué siempre debes empezar por la derecha en lugar de por la izquierda.

5. Haz la suma 7 + 5 y aprende qué hacer con la respuesta. 7+5=12, pero solo colocas el 2 debajo de la línea y el primer dígito, 1, colocarte sobre el segundo par de números, 5+3.

6. Haz la suma 1+5+3 para obtener el siguiente dígito de la respuesta. Ahora tiene 3 dígitos para sumar, porque le agregó el 1. La respuesta es 9, entonces tu respuesta hasta ahora es92.

7. Completa la tarea como de costumbre. Siga calculando las sumas de derecha a izquierda hasta que termine, agregando otra columna en este caso. tu respuesta final es 992.
Método 4 de 5: restar números enteros positivos grandes

1. Escribe la suma 4713 - 502 con el primer número encima del segundo. Escríbalo de modo que el 3 esté directamente encima del 2, el 1 esté encima del 0, el 7 esté encima del 5 y el 4 esté encima del espacio vacío.
- Puedes colocar un 0 debajo de 4 si esto te ayuda a alinear ambos números. Un cero delante de un número no cambia el valor de ese número. Un cero después de que lo haga, así que no pongas el cero allí.

2. Reste cada número inferior del número inmediatamente superior, comenzando en el extremo derecho. Resuelva los siguientes problemas en sucesión: 3-2, 1-0, 7-5 y 4-0. Coloque las respuestas directamente debajo del par de números al que pertenece.

3. Ahora haz el ejercicio 924 - 518 de la misma manera. Estos números tienen la misma longitud, por lo que puede alinearlos fácilmente. Este ejercicio te enseñará algo nuevo sobre la resta de números enteros (con suerte).

4. El primer problema, 4 - 8. Este es complicado, porque 4 es menor que 8, pero no vamos a usar números negativos. He aquí cómo resolver esto:

5. Ahora resuelve el problema 14 - 8 y escribe la respuesta debajo de la columna derecha. Ahora debería ver un 6 en el extremo izquierdo debajo de la línea.

6. Resuelva la siguiente columna (a la izquierda) con el nuevo número (el 2 fue reemplazado por un 1). Entonces esto se convierte en 1 - 1, que es igual a 0.

7. Completa el problema resolviendo la última columna. 9 - 5=4, entonces la respuesta es 406.

8. Ahora pasamos a un problema donde restamos un número más grande de un número más pequeño. Supongamos que tienes 415.990 – 968.772 debe resolver. Escribes el segundo número debajo del primero, luego te das cuenta de que el número de abajo es más grande!

9. Escribe el número más pequeño debajo del número más grande y pon un signo menos delante de la respuesta. Cada vez que restas un número de un número más pequeño, obtienes un número negativo como respuesta. Lo mejor es anotar el signo menos antes de resolver el problema para que no se te olvide.

10. Para encontrar la respuesta, resta el número pequeño del número más grande. No olvides el signo menos. Tu respuesta será negativa, como indicaste con el signo menos. Tratar no restar un número mayor de un número menor y luego hacerlo negativo; por eso no obtendrás la respuesta correcta.
Método 5 de 5: sumar y restar números enteros negativos

1. Más información sobre cómo sumar un número negativo y uno positivo. Sumar un número entero negativo es lo mismo que restar un número positivo. Esto es más fácil de ver probándolo con el método de la recta numérica como se describe en otra sección, pero también puedes pensarlo con palabras. Un número negativo no es una cantidad normal; es menor que cero y puede representar una cantidad que se quita. si te gusta esto "dispersar" cantidad a un número regular, luego lo haces más pequeño.
- Ejemplo: 10 + -3 = 10 - 3 = 7
- Ejemplo: -12 + 18 = 18 + -12 = 18 – 12 = 6. Recuerda que siempre puedes cambiar el orden de los números además, pero no al restar.

2. Aprende qué hacer cuando se convierte en una suma menos con el número más pequeño. A veces puede suceder que convertir una suma en una suma menos dé resultados como 4 – 7. Si esto sucede, invierta los números y haga que la respuesta sea negativa.

3. Aprende a sumar dos enteros negativos. Dos números negativos sumados siempre hacen que la respuesta sea negativa y mayor. No se le agrega nada positivo, por lo que siempre terminas con algo aún más alejado de cero. Encontrar la respuesta es fácil:

4. Aprende a restar un entero negativo. Al igual que con las sumas positivas, puede reescribirlas para que solo se trate de números positivos. Si restas un número negativo, entonces "te quitas algo" por "algo que se quita", que es lo mismo que sumar un número positivo.
Consejos
- Probablemente estés acostumbrado a escribir números largos como 2.521.301. En muchos países es común usar una coma en lugar de un punto, o viceversa (para decimales). No dejes que eso te confunda cuando busques información en Internet sobre este tema. Cíñete a lo que aprendas sobre esto en la escuela.
- Crear diferentes rectas numéricas para diferentes números. No es una regla que las rectas numéricas siempre vayan sobre números enteros. Esto también puede ser sobre decenas o fracciones. Excepto que cada espacio ahora representa algo diferente, aún puedes usar la recta numérica para sumar y restar de la misma manera. Darle una oportunidad.
- Si intentó el problema adicional en la sección de números grandes, aquí están las respuestas: 974 + 568 = 1542. La respuesta a la suma 415.990 – 968.772 es -552.782.
Artículos sobre el tema. "Sumar y restar números enteros"
Оцените, пожалуйста статью
Popular