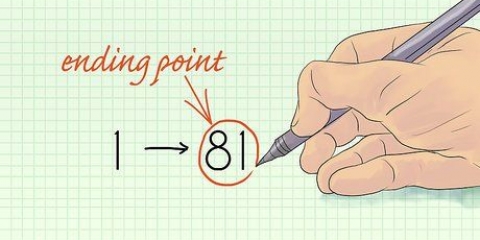
Aunque el 5 está en medio de los números 1-9, el número 5 necesita otro número para decidir cómo redondearlo. Aunque tus profesores no siempre aplican esto cuando te califican! 
Dejar todo igual y poner a cero los números a la derecha del dígito redondeado hace que el número final sea más pequeño que el original. 

7.891 -- > 7.900 15.753 --> 15.800 99. 961 --> 100.000 3.350 --> 3.300 450 --> 500 
8.800 --> 9.000 1.015 --> 1.000 12.450 --> 12.000 333.878 --> 334.000 400.400 --> 400.000 

1.239 redondeado a 3 dígitos significativos es 1.24. Esto es correcto porque el dígito a la derecha del tercer dígito (3) es un 9 (más de 5). 134.9 redondeado a 1 dígito significativo es 100. Esto es correcto porque el dígito a la derecha de la centena (1) es un 3 (menos de 5). 0.0165 redondeado a 2 dígitos significativos es 0.017. Esto es correcto porque el segundo dígito significativo es igual a 6, y el número a la derecha es un 5, así que redondeando hacia arriba. 
13,214 + 234,6 + 7,0350 + 6,38=261,2290 Tenga en cuenta que el segundo número, 234,6, solo tiene una precisión de una décima y tiene cuatro dígitos significativos. Redondea la respuesta para que la respuesta tenga la misma precisión, es decir, a la décima más cercana o a un lugar decimal. 261.2290 luego se convierte en 261.2. 
16,235 × 0,217 × 5=17,614975 Tenga en cuenta que el número 5 tiene sólo un dígito significativo. Esto significa que la respuesta final solo puede tener un dígito significativo. 17.614975 redondeado a un dígito significativo luego se convierte en 20.
Redondeo de números
Contenido
El redondeo hace que los números tengan menos decimales. Aunque los números redondeados son menos precisos que los números sin redondear, en muchos casos se prefieren. Dependiendo de la situación, puede ser necesario redondear decimales o números enteros. Si quieres aprender a redondear números, sigue estos pasos.
Pasos
Método 1 de 3: redondeo de decimales

1. Determine el número de lugares decimales de los dígitos después del punto decimal, al que debe redondear el número. Esto puede ser determinado por tu maestro, o puedes inferirlo del contexto y el tipo de números con los que estás tratando. Por ejemplo, cuando se trata de dinero, lo más probable es que desee redondear a la centésima o al centavo, mientras que con un peso necesita redondear a gramos.
- Cuanto menos preciso debe ser el número, menos dígitos hay después del punto decimal.
- Cuanto más preciso, más dígitos después del punto decimal.

2. Determinar el número de dígitos después del punto decimal. es el numero 10.7659 dado y desea redondearlo a una milésima, entonces habrá 3 dígitos después del punto decimal. Otro enfoque es redondear el número a 5 dígitos significativos. Pero primero observe la 5 del numero.

3. Encuentra el número inmediatamente a la derecha del número a redondear (el 5). ese es el numero 9. Este número determina si el 5 se redondea hacia arriba o hacia abajo.

4. Redondee hacia arriba el dígito a redondear (el dígito relevante) si el dígito a la derecha es 5, 6, 7, 8 o 9. A esto se le llama redondeo, porque el número al que se redondea es mayor que el número a redondear. La figura relevante 5, se convierte ahora 6. Todos los dígitos a la izquierda de este dígito siguen siendo los mismos, y los dígitos a la derecha desaparecen (ya no importan, simplemente igualarlos a cero). Entonces, el número 10.7659 se vuelve igual a después de redondear a la milésima más cercana 10.766.

5. Redondea hacia abajo un dígito si el dígito a la derecha es 0, 1, 2, 3 o 4. Esto significa que la cifra relevante simplemente permanece igual, aunque esto se llama redondeo hacia abajo. Nunca se puede cambiar un número a un número más bajo. por ejemplo tienes el numero 10.7653, entonces redondearías esto a 10.765 porque el grado 3 en el lado derecho de la 5 es menos de 5.
Método 2 de 3: redondear números enteros

1. Redondear un número a la siguiente decena. Para hacer esto, mira el número a la derecha de la decena. La decena es la segunda cifra, vista de derecha a izquierda, de un número. (Toma 12, entonces 1 es la decena.) Luego, si ese número está entre 0 y 4, deje el dígito para redondear sin cambios; si está entre 5-9, redondea este número 1. Aquí hay unos ejemplos:
- 12 --> 10
- 114 --> 110
- 57 --> 60
- 1,334 --> 1330
- 1,488 --> 1490
- 97--> 100

2. Redondear un número a la centena siguiente. Siga el mismo protocolo que antes con los diez. Compruebe la centena, el tercer dígito de un número, a la izquierda de la decena. (En el número 1.234, 2 es la centena). Luego use el número a la derecha de la centena, la decena, para determinar si redondear hacia arriba o hacia abajo, con los números posteriores iguales a cero. Aquí hay unos ejemplos:

3. Redondear un número al próximo millar. Las mismas reglas se aplican aquí de nuevo. Encuentra el millar y luego revisa la centena antes de redondear. Si el número está entre 0 y 4, redondea hacia abajo y si está entre 5 y 9, redondea hacia arriba. Aqui hay algunos ejemplos mas:
Método 3 de 3: redondear números a dígitos significativos

1. Trate de entender qué es un número significativo. Considere un dígito significativo como un "interesante" o un "importante" número que proporciona información útil sobre un número. Esto significa que todos los ceros a la derecha de los números enteros o a la izquierda de los decimales se pueden omitir, ya que solo llenan el espacio. Para encontrar el número de dígitos significativos en un número, simplemente cuente el número de dígitos de izquierda a derecha. Aquí están algunos ejemplos:
- 1,239 tiene 4 dígitos significativos
- 134.9 tiene 4 dígitos significativos
- 0.0165 tiene 3 dígitos significativos

2. Redondear un número a un número de dígitos significativos. Esto depende de la tarea en la que estés trabajando. Por ejemplo, si redondea un número a dos dígitos significativos, debe tratar de reconocer el segundo dígito significativo del número y luego usar el número de la derecha para determinar si redondear hacia arriba o hacia abajo. Aquí hay unos ejemplos:

3. Redondee al número correcto de cifras significativas al sumar. Para hacer esto, primero es necesario sumar los números dados. Luego encuentre el número con el menor número de dígitos significativos y redondee su respuesta a ese número. Así es como funciona:

4. Redondea al número correcto de dígitos significativos al multiplicar. Primero multiplica todos los números dados. Luego verifique cuál de los números se redondea al menor número de dígitos significativos. Finalmente, redondea la respuesta con el mismo grado de precisión que ese número. Así es como funciona:
Consejos
- Es común omitir los ceros a la derecha de un decimal después de redondear. Los ceros a la derecha de un decimal no cambian el valor del número. Es por eso que deben dejarse de lado. Esto no se aplica a los ceros a la izquierda de (antes) de un decimal.
- Una vez que haya encontrado el número relevante para redondear, subráyelo. Esto asegura que no haya confusión sobre el número que va a redondear y el número al que se redondea ese número relevante.
Advertencias
- Asegúrese de estar familiarizado con la terminología. La diferencia entre decenas y décimas, centenas y centésimas, decimales, decimales, significado, etc...
Artículos sobre el tema. "Redondeo de números"
Оцените, пожалуйста статью
Popular