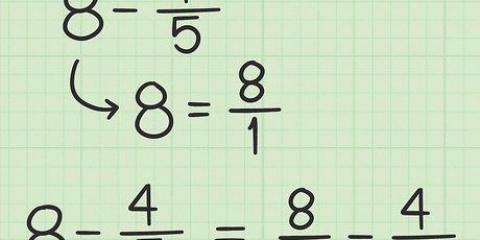Restar números

Contenido

Pasos
Consejos
Advertencias

Las restas son aquellas sumas en las que restas dos números entre sí. Es bastante simple si desea restar números enteros entre sí, pero se vuelve un poco más complicado cuando trabaja con fracciones o decimales. Una vez que haya dominado la resta, puede pasar a los conceptos matemáticos más complicados y sumar, multiplicar y dividir números será mucho más fácil.

Pasos

Método 1 de 6: Resta números enteros grandes tomando prestados

1. Escribe el número mayor. Suponga que trabaja con la suma 32 - 17. Escribe 32 primero.

2. Escribe el número más pequeño directamente debajo de él. Asegúrese de que las decenas y las unidades estén bien alineadas para que las 3 pulgadas "32" directamente por encima de 1 en "17" estado, y los 2 en "32" directamente encima de la "7" a los 17.

3. Resta el número de abajo del de arriba. Esto puede ser un poco complicado si el número de abajo es mayor que el de arriba. En este caso 7 es mayor que 2. Esto es lo que debe hacer:

tendras que "a prestar" de los 3 en "32" para hacer el 2 un 12.

Cruza los 3 de "32" y convertirlo en 2, luego convertir la unidad 2 en 12.

Ahora tienes 12 – 7 = 5. Escribe un 5 debajo de la columna de unidades.

4. Resta la decena del número de abajo de la decena del número de arriba. No olvides que el 3 de 32 se ha convertido en 2. Ahora resta el 1 en 17 del 2 de arriba, entonces 2-1 = 1. Escribe 1 debajo de la columna de las decenas. Si todo está bien, ahora tienes 15 como respuesta, entonces 32 - 17 = 15.

5. Revisa tu trabajo. Si quieres asegurarte de haber hecho el cálculo correctamente, todo lo que necesitas hacer es sumar la respuesta al número más pequeño para recuperar el número más grande. Para verificar: 15 + 17 = 32, entonces lo hiciste bien. Excelente!

Método 2 de 6: Resta números enteros pequeños

1. Determinar qué número es mayor. Un ejercicio como 15 - 9 requiere un enfoque diferente que 2 - 30.

En la suma 15 - 9, el primer número, 15, es el más grande.
En la suma 2 - 30, el segundo número, 30 es el mayor.

2. Decide si tu respuesta debe ser positiva o negativa. Si el primer numero es el mas grande entonces la respuesta es positiva. Si el segundo número es el mayor, la respuesta es negativa.

Entonces en la primera suma, 15 - 9, la respuesta se vuelve positiva, porque 15 es mayor que 9.

Entonces, en la segunda suma, 2 - 30, la respuesta se vuelve negativa, porque 2 es menor que 30.

3. Encuentra la diferencia entre los dos números. Para restar dos números, calcula la diferencia entre ellos.

Para el problema 15 - 9, toma 15 monedas. Quita 9 y cuenta cuantos quedan (6). Entonces, 15 - 9 = 6. O usa una recta numérica y dibuja los números del 1 al 15 a lo largo de la recta, luego tacha el 9 del 15 hacia abajo para llegar al 6.

Con la suma 2 – 30 es más fácil invertir los números y hacer que la respuesta sea negativa. Entonces, 30 - 2 = 28, y con eso 2 - 30 es -28.

Método 3 de 6: Restar decimales

1. Escribe el número mayor encima del número menor para que los decimales queden alineados. Suponga que tiene el siguiente problema: 10.5 - 8.3. Escribe el 10.5 arriba del 8.3 de tal forma que las comas queden una encima de la otra.

Si tiene un problema donde un número tiene más decimales que el otro, llene el espacio vacío con ceros. Por ejemplo, si tiene el problema 5.32 - 4.2, puede reescribirlo como 5.32 = 4.20. Esto no cambia el valor de un número, pero te aseguras de que ambos números se puedan restar más fácilmente entre sí.

2. Restar las décimas entre sí. La resta de estos números es igual que con los enteros, excepto que debes prestar atención al punto decimal, alineado e incluido en la respuesta. En este caso hay que restar 3 de 5. 5 - 3 = 2, entonces escribes un 2 debajo del 3 en 8.3.

No olvides incluir el punto decimal (la coma) en la respuesta. Ahora se ve así: ,2.

3. Ahora resta las unidades entre sí. Ahora resta 8 de 0. Toma prestada una docena del 1 (al lado del 0) para hacer 10, ahora resta 8 de 10. También puede calcular inmediatamente la suma 10 – 8 = 2, sin el paso intermedio de pedir prestado, porque el número de abajo no tiene diez. Escribe la respuesta debajo de 8.

4. Así que la respuesta final será 2.2.

Método 4 de 6: restar fracciones

1. Pon los numeradores y los denominadores juntos. Suponga que está trabajando con el problema 13/10 - 3/5. Escribe este problema de modo que ambos numeradores, 13 y 3, y ambos denominadores, 10 y 5, estén uno al lado del otro, separados por un signo menos. Esto le da una mejor visión general del problema y hace que sea más fácil encontrar una solución.

2. Encuentra el mínimo común múltiplo. Este es el múltiplo más pequeño de dos números. El LCF de 10 y 5 en este ejemplo es 10.

Tenga en cuenta que el mcm de dos números no siempre es uno de los dos números. Por ejemplo, en 3 y 2, el LCF es 6, porque no hay número menor que 6 que sea múltiplo de cada uno de los números.

3. Reescribe las fracciones con los mismos denominadores. La fracción 13/10 puede permanecer sin cambios porque el denominador no ha cambiado, pero la fracción 3/5 se vuelve igual a 6/10 porque el denominador va dos veces al común múltiplo de 10. Ahora has igualado ambas fracciones. 3/5 es igual a 6/10, pero con la diferencia de que ahora ya no es un problema restar ambas fracciones entre sí.

Así que la nueva tarea será: 13/10 - 6/10.

4. Restar ambos numeradores entre sí. Entonces 13 - 6 = 7. No restes los denominadores.

5. Coloque el nuevo numerador sobre el nuevo denominador (el LCF previamente calculado) para la respuesta final. El nuevo numerador es 7 y el denominador de ambas fracciones es 10. Entonces la respuesta final es 7/10.

6. Revisa tu trabajo. Si quieres asegurarte de haber hecho el cálculo correctamente, todo lo que necesitas hacer es sumar la respuesta al número más pequeño para recuperar el número más grande. Para comprobar: 7/10 + 6/10 = 13/10. Ya está todo listo.

Método 5 de 6: Resta una fracción de un número entero

1. escribir la tarea. Supongamos que tenemos el siguiente problema: 5 - 3/4. Tenga en cuenta esto.

2. Convierte el número entero en una fracción con el mismo denominador que la fracción dada. Haz una fracción del 5 con el denominador 4. Primero considera que 5 es igual a la fracción 5/1. Luego, multiplicas tanto el numerador como el denominador de la nueva fracción por 4 para obtener dos fracciones con el mismo denominador. Esto mantiene el valor de la fracción igual, pero con números diferentes. Entonces, 5/1 x 4/4 = 20/4.

3. Reescribir la tarea. Esto ahora se puede escribir como: 20/4 - 3/4.

4. Resta los numeradores de las fracciones y mantén las fracciones iguales. Entonces, 20 - 3 = 17. Entonces el numerador final se convierte en 17 y el denominador es 4.

5. Entonces la respuesta al problema es 17/4. Para convertir esta fracción impropia en una fracción compuesta, divide 17 entre 4 para obtener el número 4 con un resto de 1. La respuesta entonces se ve así: 4 1/4.

Método 6 de 6: Resta de variables

1. escribir la tarea. Suponga que está trabajando en el siguiente problema: 3x - 5x + 2y - z - (2x + 2x + y). Escribe la primera ecuación encima de la segunda.

2. Resta todos los términos semejantes entre sí. Al trabajar con variables, solo puede restar términos con la misma variable y con el mismo poder. Esto significa que puedes hacer 4x -7x, pero no 4x -7x. Entonces puedes dividir esta tarea así:

3x - 2x = x

-5x - 2x = -7x

2y - y = y

-z - 0 = -z

3. da tu respuesta final. Ahora que ha restado todos los términos iguales, puede dar inmediatamente su respuesta final. Aquí está la respuesta:

3x - 5x + 2y - z - (2x + 2x + y) = x - 7x + y - z

Consejos

Dividir números más grandes en partes más pequeñas. Tomar: 63 - 25.Nadie dice que tienes que restar los 25 a la vez. Primero puedes restar 3 para obtener 60; luego restar 20 para obtener 40 y luego los últimos 2. resultado: 38. Y ahora no tienes que pedir prestado.

Advertencias

Si tiene una mezcla de números positivos y negativos, las cosas se vuelven mucho más complicadas.Sigue buscando artículos que te puedan ayudar con esto.