Por ejemplo: en la fracción 1/5, 1 es el numerador. 
Por ejemplo: en la fracción 1/5, 5 es el denominador, entonces la fracción consta de cinco partes. 
Por ejemplo: 3/4 es una fracción real y 5/3 es una fracción impropia. Si tienes un número entero con una fracción, se llama fracción mixta. Por ejemplo: 1 1/2 es una fracción mixta. 

Por ejemplo, para encontrar un factor común para 1/3 + 2/5, multiplique el 1 y el 3 por 5 y multiplique el 2 y el 5 por 3. Entonces obtienes 5/15 + 6/15. Ahora puedes sumar las fracciones. 
Por ejemplo: 3/6 - 2/6=1/6. No sumar (o restar) los denominadores. 


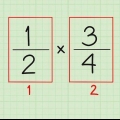
Por ejemplo, para multiplicar 1/3 por 3/4, multiplica 1 por 3 para obtener el numerador. Luego multiplica 3 por 4 para obtener el denominador. Tu respuesta es entonces 3/12. 
Por ejemplo, si su respuesta es 3/12, entonces 3 es el máximo común divisor. Simplifica la fracción por 3 para obtener 1/4. 

Para continuar con el ejemplo, multiplica 5/4 por 2/1 para obtener 10/4. 
Por ejemplo, el máximo común divisor de 10/4 es 2, por lo que su respuesta simplificada es 5/2. Si esta es una fracción impropia, conviértala en un número entero con una fracción. 5/2 luego se convierte en 2 1/2.
Calcular con fracciones
Contenido
Contar con fracciones es una de las habilidades matemáticas más útiles para desarrollar. Antes de empezar, aprende a reconocer las diferentes partes y tipos de fracciones. Luego puedes seguir sumando y restando fracciones. Puede que le resulte más difícil multiplicarlos y dividirlos. En la mayoría de los casos, también deberá simplificar o reducir la fracción.
Pasos
Método 1 de 4: identificar las partes de una fracción

1. hacer una fracción. Las fracciones se escriben como dos números uno debajo del otro, separados por un guión.

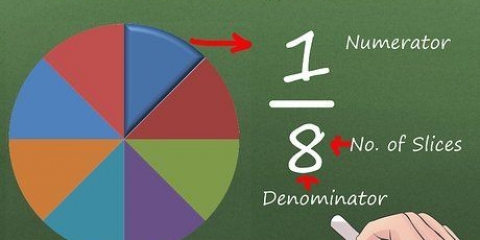
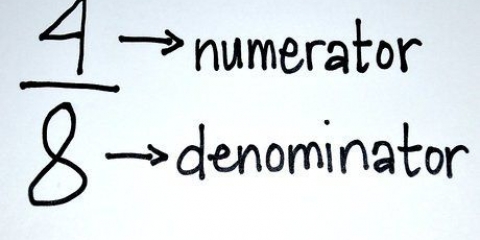
2. Encuentra el mostrador. El número en la parte superior se llama numerador y te dice cuántas partes de la fracción hay.

3. Encuentra el denominador. El número debajo de la barra de división se llama denominador. Este número indica qué tipo de fracción es.

4. Determinar si la fracción es real (actual) o falsa (impropia). Si el numerador es menor que el denominador, entonces la fracción es real. En una fracción impropia el numerador es mayor que el denominador.
Método 2 de 4: sumar o restar fracciones

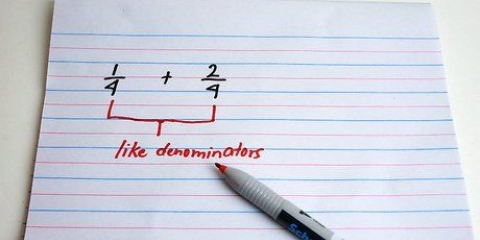
1. Reconocer fracciones con denominadores similares. Si necesita sumar o restar fracciones, deben tener denominadores comunes antes de hacer sus cálculos. Mira el denominador de cada fracción para ver si son iguales (comunes).

2. Encuentra un denominador común si los denominadores son diferentes. Si los denominadores no son iguales, debes cambiar las fracciones para que tengan los mismos denominadores. Para encontrar un denominador común, multiplica el numerador y el denominador de una fracción por el denominador de la otra fracción.

3. Calcular la fracción sumando o restando. Una vez que haya encontrado un denominador común y haya multiplicado los números según sea necesario, estará listo para sumar o restar las fracciones. Suma o resta los numeradores y coloca la suma encima de una división. Poner el común denominador debajo de la línea de división.

4. Simplifica la suma si es necesario. Si tuviera que encontrar un denominador común, podría terminar con una fracción grande que se puede simplificar. Por ejemplo, si sumas 8/32 +12/32, obtienes 20/32. Esto se puede simplificar a 5/8.
Método 3 de 4: multiplicar y simplificar fracciones

1. Convertir fracciones mixtas o enteros a fracciones impropias. Para que sea más fácil multiplicar, debes trabajar con fracciones reales o impropias. Si tienes un número entero o una fracción mixta que quieres multiplicar, hazlo una fracción.
- Por ejemplo, para multiplicar 2/5 por 7, convertirías 7 en una fracción. Entonces puedes multiplicar 2/5 por 7/1.
- Si tienes una fracción mixta como 1 1/3, conviértela en una fracción impropia (4/3) antes de multiplicar.

2. Multiplicar los numeradores y los denominadores. En lugar de sumar los numeradores, multiplícalos y escribe el resultado sobre una línea de división. También debes multiplicar los denominadores y poner el resultado debajo de la línea de división.

3. Simplifica el resultado. En muchos casos, deberá reducir el resultado a una fracción simplificada, especialmente si comenzó con fracciones impropias. Encuentra el máximo común divisor y úsalo para simplificar el numerador y el denominador.
Método 4 de 4: dividir fracciones

1. Invertir la segunda fracción. La forma más fácil de dividir fracciones, incluso las que tienen un denominador diferente, es voltear la segunda fracción antes de calcular la suma.
- Por ejemplo: con 5/4 ÷ 1/2 necesitas voltear el 1/2 a 2/1.

2. Multiplicar los numeradores y los denominadores. Multiplica las fracciones (no en cruz) para multiplicar los numeradores. Pon el resultado encima de la división de fracciones y multiplica los denominadores. Poner el resultado debajo de la línea de división.

3. Simplificar los resultados, si es necesario. Si tu respuesta es una fracción impropia o se puede simplificar, simplifica la fracción. Usa el máximo común divisor para simplificar la fracción.
Consejos
- Si está trabajando con fracciones apiladas, deberá realizar algunos pasos adicionales para obtener simplificarlos, pero sigue siendo una parte necesaria de la elaboración.
- Siempre escriba sus fracciones cuidadosamente para reducir la posibilidad de errores de cálculo.
Artículos sobre el tema. "Calcular con fracciones"
Оцените, пожалуйста статью
Popular