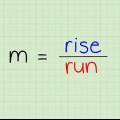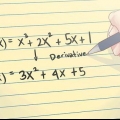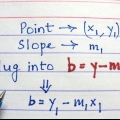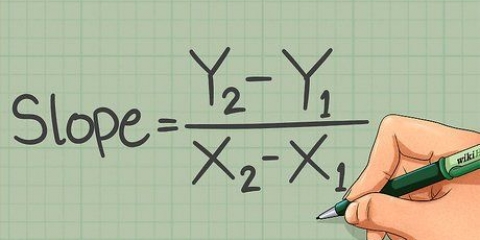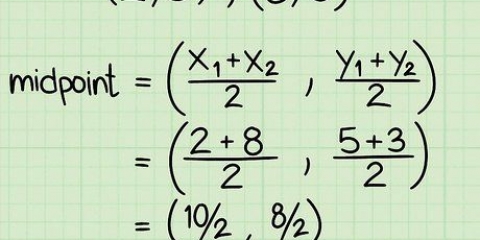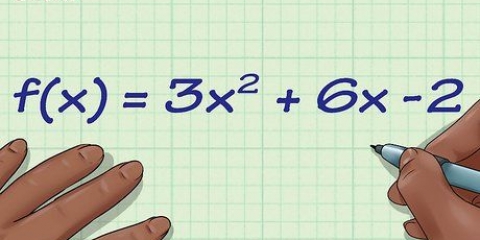Pendiente = 2 
Pendiente = -1 
pendiente = 

Encuentre la pendiente de 
Conviértelo a la forma  :
: 



Determinar la pendiente: Pendiente = M = 4 

En cada par, la coordenada x es el primer número y la coordenada y es el segundo número después del punto decimal. Cada coordenada x en una línea tiene una coordenada y correspondiente. 
X1: 2 y1: 4 X2: 6 y2: 6 
Puntos originales: (2.4) y (6.6). Aplicar a la fórmula punto-pendiente: 
Simplifique para la respuesta final:  = pendiente
= pendiente



Con este método, hazte la siguiente pregunta: "¿Cuál es la pendiente de la recta?  en el punto (4.2)?"
en el punto (4.2)?" La derivada a menudo se escribe como ![Determinar la pendiente de una recta f` origen=]() o
o 
4 X + 6 

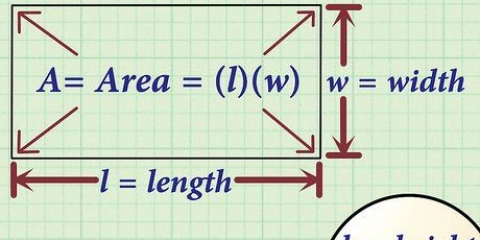
Determinar la pendiente de una recta
Contenido
La pendiente de una línea es una medida de qué tan rápido cambia la línea. Esto se puede hacer con una línea recta, donde la pendiente te dice exactamente qué tan lejos (pendiente positiva) o hacia abajo (pendiente negativa) recorre una cierta distancia. La pendiente también se puede utilizar para una tangente a una curva. O podría ser una línea curva, utilizada en el análisis, donde la pendiente también se conoce como la "derivada" de una función. De todos modos, piense en la pendiente como la "tasa de cambio" de un gráfico: si la variable "x" aumenta, ¿a qué tasa cambia "y"?? Esa es una forma de pensar en la pendiente como causa y efecto.
Pasos
Método 1 de 3: encontrar la pendiente de una ecuación lineal

1. Use la pendiente para determinar qué tan empinada y en qué dirección (hacia arriba o hacia abajo) va una línea. Determinar la pendiente de una línea es fácil, siempre y cuando tengas o puedas dibujar una ecuación lineal. Este método solo funciona cuando:
- Las variables no tienen exponentes.
- Solo hay dos variables, y ninguna de ellas son fracciones (por ejemplo, las siguientes no pueden ser:
)
- La ecuación se puede simplificar a la forma
, por lo cual metro y B constantes (números como 3, 10, -12,
).
2. Encuentre el número antes de la x, generalmente escrito como `m` para determinar la pendiente. Si la ecuación ya está en la forma correcta,  , luego simplemente elija el número en la posición `m` (pero si no hay ningún número antes de x, entonces la pendiente es 1). Así que esa es también la pendiente! Sepa que este número, metro, siempre se multiplica por la variable, en este caso una `x`. Mira los siguientes ejemplos:
, luego simplemente elija el número en la posición `m` (pero si no hay ningún número antes de x, entonces la pendiente es 1). Así que esa es también la pendiente! Sepa que este número, metro, siempre se multiplica por la variable, en este caso una `x`. Mira los siguientes ejemplos:
 , luego simplemente elija el número en la posición `m` (pero si no hay ningún número antes de x, entonces la pendiente es 1). Así que esa es también la pendiente! Sepa que este número, metro, siempre se multiplica por la variable, en este caso una `x`. Mira los siguientes ejemplos:
, luego simplemente elija el número en la posición `m` (pero si no hay ningún número antes de x, entonces la pendiente es 1). Así que esa es también la pendiente! Sepa que este número, metro, siempre se multiplica por la variable, en este caso una `x`. Mira los siguientes ejemplos:




3. Reconocer la ecuación donde una variable está aislada si la pendiente no está clara. Puedes sumar, restar, multiplicar, etc. para aislar una variable (generalmente la `y`). Recuerda que hagas lo que hagas en un lado del signo igual (como sumar 3), también debes hacerlo en el otro lado. Su objetivo final es una ecuación, como  . Por ejemplo:
. Por ejemplo:
 . Por ejemplo:
. Por ejemplo:
 :
:



Método 2 de 3: Determinar la pendiente con dos puntos

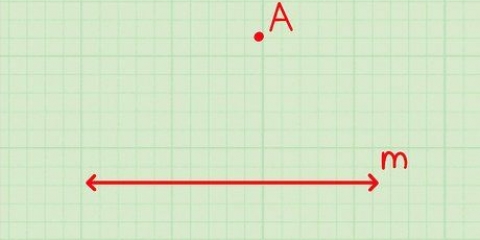
1. Usa un gráfico y dos puntos para encontrar rápidamente la pendiente sin la ecuación. Si tiene un gráfico y una línea pero no una ecuación, aún puede determinar la pendiente con facilidad. Todo lo que necesitas son dos puntos en la línea, que aplicas a la ecuación  . Al determinar la pendiente, tenga en cuenta la siguiente información para asegurarse de que está en el camino correcto:
. Al determinar la pendiente, tenga en cuenta la siguiente información para asegurarse de que está en el camino correcto:
 . Al determinar la pendiente, tenga en cuenta la siguiente información para asegurarse de que está en el camino correcto:
. Al determinar la pendiente, tenga en cuenta la siguiente información para asegurarse de que está en el camino correcto: - Las pendientes positivas van hacia arriba y hacia la derecha.
- Las pendientes negativas van hacia abajo y hacia la derecha.
- Las pendientes más empinadas son líneas más empinadas. Las pendientes menos pronunciadas son siempre más graduales.
- rectas horizontales perfectas tienen pendiente cero.
- Las líneas perfectamente verticales no tienen ninguna pendiente. Su pendiente (o pendiente) es `indefinida`.

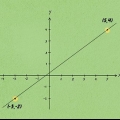
2. Elija dos puntos, colocándolos en la forma simple (x, y). Usar el gráfico (o la pregunta de la tarea) para encontrar las coordenadas x e y de dos puntos en el gráfico. Pueden estar formados por dos puntos cualesquiera por los que pasa la recta. Por ejemplo, suponga que en este método la recta pasa por el punto (2.4) y por (6.6).

3. Etiqueta los puntos x1, y1, X2, y2, y mantener cada punto con su par. Continuando con nuestro primer ejemplo, usando los puntos (2.4) y (6.6), etiqueta las coordenadas x e y de cada punto. Si todo salió bien, ahora terminas con:

4. Sustituye estos puntos en la `fórmula punto-pendiente` para encontrar la pendiente. La siguiente fórmula se usa para determinar la pendiente usando dos puntos cualquiera en una línea recta:  . Simplemente sustituya los cuatro puntos y simplifique:
. Simplemente sustituya los cuatro puntos y simplifique:
 . Simplemente sustituya los cuatro puntos y simplifique:
. Simplemente sustituya los cuatro puntos y simplifique:
 = pendiente
= pendiente
5. Comprender cómo funciona la fórmula punto-pendiente. La pendiente de una línea se indica por el cambio de y de x (y/x): cuánto sube la línea dividido por cuánto continúa la línea hacia la derecha. El aumento de la recta es la diferencia entre los valores de y (recuerda, el eje y sube y baja), y el aumento de la recta es la diferencia entre los valores de x (y el eje x va de de izquierda a derecha).

6. Aprenda otras formas que necesita saber para determinar la pendiente. La ecuación de la pendiente es  . Esto también se puede representar con la letra griega `Δ` (`delta`), que significa `diferencia`. La pendiente también se puede representar como Δy/Δx, que significa `diferencia de y` / `diferencia de x`. Esta es exactamente la misma pregunta que "Determine la pendiente entre.."
. Esto también se puede representar con la letra griega `Δ` (`delta`), que significa `diferencia`. La pendiente también se puede representar como Δy/Δx, que significa `diferencia de y` / `diferencia de x`. Esta es exactamente la misma pregunta que "Determine la pendiente entre.."
 . Esto también se puede representar con la letra griega `Δ` (`delta`), que significa `diferencia`. La pendiente también se puede representar como Δy/Δx, que significa `diferencia de y` / `diferencia de x`. Esta es exactamente la misma pregunta que "Determine la pendiente entre.."
. Esto también se puede representar con la letra griega `Δ` (`delta`), que significa `diferencia`. La pendiente también se puede representar como Δy/Δx, que significa `diferencia de y` / `diferencia de x`. Esta es exactamente la misma pregunta que "Determine la pendiente entre.."Método 3 de 3: usa el cálculo diferencial para encontrar la pendiente de una curva

1. Revisa cómo puedes determinar la derivada de funciones comunes de diferentes maneras. Los derivados te dan la tasa de cambio (o pendiente) en un punto de una recta. La línea puede ser curva o recta, no importa. Recuerde cómo cambia la línea en un momento dado, en lugar de cómo cambia la pendiente de toda la línea. Cómo determinas la derivada depende del tipo de función, así que repasa cómo determinar la derivada de funciones antes de continuar.
- Lea aquí sobre cómo determinar la derivada
- Las derivadas más simples, las de ecuaciones exponenciales estándar, usted puede encontrar fácilmente con un método rápido. Usarás esto en el resto del método.

2. Comprender qué problemas requieren que calcules la pendiente usando derivadas. No siempre se le pedirá explícitamente la derivada o la pendiente de una curva. También se le puede preguntar sobre la `tasa de cambio` en el punto (x, y). Se le puede pedir una ecuación para la pendiente de la gráfica, lo que simplemente significa encontrar la derivada. Finalmente, se le puede pedir `la pendiente de la recta tangente en (x, y)`. Esto significa nuevamente que solo solicita la pendiente de la curva en un punto específico (x, y).
 en el punto (4.2)?"
en el punto (4.2)?"
3.Encuentra la derivada de la función. Ni siquiera necesitas un gráfico real, solo la función o ecuación del gráfico. En este ejemplo usamos una función previamente discutida,


4.Sustituye el punto en la ecuación de la derivada para encontrar la pendiente. La diferencial de una función te da la pendiente de la función en un punto dado. En otras palabras, F"(x) es la pendiente de la función en cualquier momento (x,f(x)). Así que para este problema de ejercicio:
Artículos sobre el tema. "Determinar la pendiente de una recta"
Оцените, пожалуйста статью
Similar
Popular