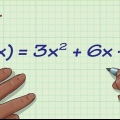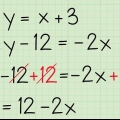Cómo determinar si dos líneas son paralelas

Contenido

Pasos

Las líneas paralelas son dos líneas en un plano que nunca se intersecarán (lo que significa que continuarán para siempre sin tocarse). Una característica importante de las rectas paralelas es que tienen pendientes idénticas. La pendiente de una línea se define como la elevación (cambio en las coordenadas y) sobre la caída (cambio en las coordenadas x) de una línea, en otras palabras, qué tan inclinada es la línea. Las líneas paralelas a menudo se representan mediante dos líneas verticales (ll). Por ejemplo, AB11CD indica que la línea AB es paralela a CD.

Pasos

Método 1 de 3: comparar la pendiente de cada línea

Imagen titulada Averiguar si dos líneas son paralelas Paso 1

1. Encuentre la fórmula para la pendiente. La pendiente (pendiente) de una línea está definida por (Y₂ - Y₁)/(X₂ - X₁) donde X e Y son las coordenadas horizontales y verticales de los puntos en la línea. Necesitas determinar dos puntos en la línea para calcular esta fórmula. El punto más cercano al final de la recta es (X₁, Y₁) y el punto más arriba en la línea, por encima del primer punto, es (X₂, Y₂).

Esta fórmula se puede reformular como el aumento sobre la distancia. Es el cambio vertical comparado con el cambio horizontal, o la inclinación de la línea.
Si una recta apunta hacia la derecha y hacia arriba, tendrá pendiente positiva.
Si la recta apunta hacia la derecha y hacia abajo, tendrá pendiente negativa.

Imagen titulada Averiguar si dos líneas son paralelas Paso 2

2. Identifique las coordenadas X e Y de dos puntos en cada línea. Un punto en una línea está dado por su coordenada (X, Y) donde X es la ubicación en el eje horizontal e Y es la ubicación en el eje vertical. Para calcular la pendiente, debe determinar dos puntos en cada una de las líneas en cuestión.

Los puntos son fáciles de determinar si ha dibujado una línea en papel cuadriculado.

Para determinar un punto, dibuje una línea de puntos desde el eje horizontal hasta que se cruce con la línea. La posición donde comenzaste la línea en el eje horizontal es la coordenada x, mientras que la coordenada y es donde la línea punteada se cruza con la línea en el eje vertical.

Por ejemplo: linea yo tiene los puntos (1, 5) y (-2, 4) mientras que la línea r tiene los puntos (3, 3) y (1, -4).

Imagen titulada Averiguar si dos líneas son paralelas Paso 3

3. Procese los puntos para cada línea en la fórmula de la pendiente. Para calcular la pendiente, ingrese los números, reste y divida. Asegúrese de insertar las coordenadas en el valor correcto de x e y en la fórmula.

A la pendiente de la recta yo para calcular: pendiente = (5 - (-4))/(1 - (-2))

Restar: pendiente = 9/3

Dividir: pendiente = 3

La pendiente de la línea r = (3 - (-4))/(3 - 1) = 7/2

Imagen titulada Averiguar si dos rectas son paralelas Paso 4

4. Compara las pendientes de cada recta. Recuerda que dos rectas solo son paralelas si tienen las mismas pendientes. Las líneas pueden parecer paralelas en el papel e incluso estar muy cerca de ser paralelas, pero si sus pendientes no son exactamente iguales, no son paralelas.

En este ejemplo, 3 no es igual a 7/2, por lo que estas dos líneas no son paralelas.

Método 2 de 3: usar la fórmula de pendiente e intersección

Imagen titulada Averiguar si dos rectas son paralelas Paso 5

1. Encuentre la fórmula para la pendiente y la intersección de una línea. La fórmula de la pendiente, la ecuación de una línea recta. es y = mx + b, donde m es la pendiente, b es la intersección con el eje y, y x e y son variables que representan coordenadas en la línea, generalmente las ves como x e y en la ecuación. De esta forma, puede determinar fácilmente la pendiente de la línea como la variable `m`.

Un ejemplo: reescribe 4y - 12x = 20 y y = 3x -1. La ecuación 4y - 12x = 20 debe reescribirse con álgebra mientras que y = 3x -1 ya tiene la forma de la fórmula de la pendiente y no necesita reescribirse.

Imagen titulada Averiguar si dos rectas son paralelas Paso 6

2. Reescribe la fórmula de la línea como fórmula de pendiente. A menudo, la fórmula de la línea que obtienes no tendrá la forma de un plano inclinado. Solo se necesita un poco de matemática y reorganización de variables para que tenga la forma de fórmula de pendiente.

Por ejemplo: Reescriba la línea 4y-12x=20 como fórmula de pendiente.

Suma 12x a ambos lados de la ecuación: 4y - 12x + 12x = 20 + 12x

Divide cada lado por 4 para aislar y: 4y/4 = 12x/4 +20/4

Fórmula de la pendiente: y = 3x + 5

Imagen titulada Averiguar si dos rectas son paralelas Paso 7

3. Compara las pendientes de cada recta. Recuerda que si dos rectas son paralelas entre sí, tendrán exactamente la misma pendiente. Usando la ecuación y = mx + b, donde m es la pendiente de la recta, puedes determinar y comparar las pendientes de dos rectas.

En nuestro ejemplo, la primera línea tiene una ecuación de y = 3x + 5, por lo que la pendiente es 3. La otra línea tiene una ecuación de y = 3x - 1 que también tiene una pendiente de 3. Como las pendientes son idénticas, estas dos rectas son paralelas.

Tenga en cuenta que si estas ecuaciones tienen la misma intersección con el eje y, serían la misma línea en lugar de paralelos.

Método 3 de 3: determinar una recta paralela con la ecuación punto-pendiente

Imagen titulada Averiguar si dos líneas son paralelas Paso 8

1. Definir la ecuación punto-pendiente. Con la ecuación punto-pendiente puedes escribir la ecuación de una recta si conoces la pendiente y tienes una coordenada (x, y). Utiliza esta fórmula si desea definir una segunda línea paralela en una línea ya dada con una pendiente determinada. La fórmula es y – y₁= m(x – x₁) donde m es la pendiente de la recta, x₁ la coordenada x de un punto dado en la línea y y₁ la coordenada y de ese punto. Como en la fórmula de la pendiente, x e y son variables que representan coordenadas en la línea; por lo general, permanecerán como x e y en la ecuación.

Los siguientes pasos resuelven este ejemplo: Escribe la ecuación de una recta paralela a la recta y = -4x + 3 que pasa por el punto (1, -2).

Imagen titulada Averiguar si dos rectas son paralelas Paso 9

2. Encuentre la pendiente de la primera línea. Al escribir la ecuación de una nueva recta, primero debes determinar la pendiente de la recta a la que tu recta debe ser paralela. Asegúrate de que la ecuación de la línea original sea una fórmula de pendiente para que sepas la pendiente (m) de inmediato.

La recta que queremos hacer paralela es y = -4x + 3. En esta ecuación -4 representa la variable m y por tanto la pendiente de la recta.

Imagen titulada Averiguar si dos líneas son paralelas Paso 10

3. Identificar un punto en la nueva línea. Esta ecuación solo funciona si tienes una coordenada que pasa por la nueva línea. Asegúrese de no elegir una coordenada que esté en la línea original. Si sus ecuaciones finales tienen la misma intersección con el eje y, no son paralelas, sino la misma línea.

En nuestro ejemplo usamos la coordenada (1, -2).

Imagen titulada Averiguar si dos rectas son paralelas Paso 11

4. Escribe la ecuación de la nueva línea en la forma punto-pendiente. Recuerda que la fórmula es: y – y₁= m(x – x₁). Ingrese la pendiente y las coordenadas de su punto para hacer que la ecuación de su nueva línea sea paralela a la primera.

Usando nuestro ejemplo con pendiente (m) -4 y (x, y) coordenada (1, -2) esto se convierte en: y – (-2) = -4(x – 1)

Imagen titulada Averiguar si dos rectas son paralelas Paso 12

5. Simplifica la ecuación. Después de completar los números, la ecuación se puede simplificar a la fórmula de pendiente más común. La línea de esta ecuación, cuando se dibuja en un sistema de coordenadas, es paralela a la ecuación dada.

Por ejemplo: y - (-2) = -4(x - 1)

Dos negativos hacen un positivo: y + 2 = -4(x -1)

Usa la propiedad distributiva para calcular -4(x -1): y + 2 = -4x + 4.

Resta -2 de ambos lados: y + 2 - 2 = -4x + 4 - 2

La ecuación simplificada: y = -4x + 2