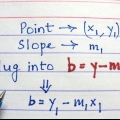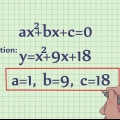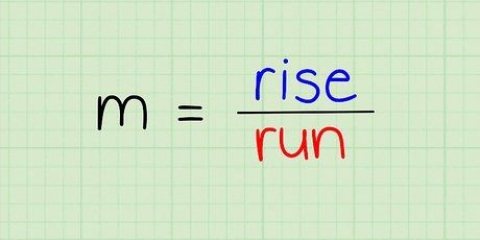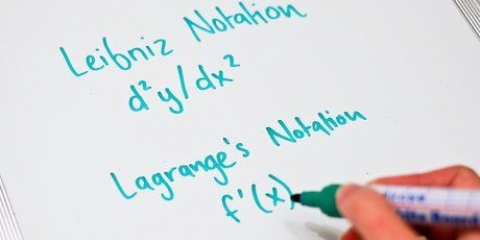Hallar la ecuación de una recta tangente: 4 pasos (con fotos)

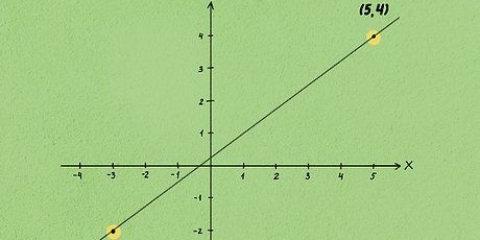
Una tangente a una parábola o curva es una línea que solo toca la curva en un punto dado. Para encontrar la ecuación de esta recta tangente, tendrás que calcular la pendiente de la curva en ese punto, lo que requiere algunos cálculos matemáticos. A continuación, puede escribir la ecuación de la línea tangente en forma de punto-pendiente. Este artículo explica los pasos a seguir.

Pasos

Imagen titulada Encuentra la ecuación de una recta tangente Paso 1

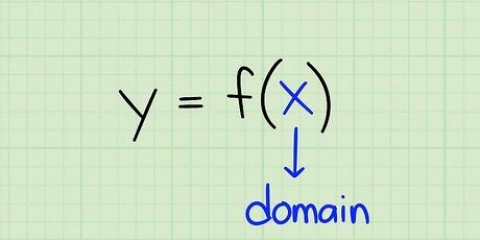
1. La ecuación de una curva se puede expresar como una función. Encuentra la derivada de esta función para encontrar la ecuación de la pendiente de esta curva.

La forma más fácil de diferenciar la mayoría de los polinomios es a través de la regla de la cadena. Multiplica cada ecuación de la función por su potencia para encontrar el coeficiente de ese término en la derivada, luego resta la potencia por 1.
Ejemplo: Para la función f(x) = x^3 + 2x^2 + 5x + 1, la derivada es f`(x) = 3x^2 + 4x + 5.
Para f(x) = (2x+5)^10 + 2*(4x+3)^5, la derivada es f`(x) = 10*2*(2x+5)^9 + 2*5*4 *(4x+3)^4 = 20*(2x+5)^9 + 40*(4x+3)^4.

Imagen titulada Encuentra la ecuación de una recta tangente Paso 2

2. Si todo está bien, se dan las coordenadas donde la recta tangente se encuentra con la curva. Reemplaza el valor de x de este punto, en la función derivada, para encontrar la pendiente de la curva en ese punto.

Para x = 2, el punto de la curva es (2.27) porque f(2) = 2^3 + 2*2^2 + 5*2 + 1 = 27.

Para f`(x) = 3x^2 + 4x + 5, la pendiente está en (2.27) es f`(2) = 3(2)^2 + 4(2) + 5 = 25.

Imagen titulada Encuentra la ecuación de una recta tangente Paso 3

3. Esta pendiente es también la pendiente de la recta tangente. Ahora que tienes la pendiente y el punto de esta línea, puedes escribir la ecuación de la línea en forma de punto-pendiente, o y - y1 = m(x - x1).

En la forma punto-pendiente, es metro la pendiente y (x1,y1) son las coordenadas del punto. Entonces, en este ejemplo, la ecuación se convierte en y - 27 = 25(x - 2).

Imagen titulada Encuentra la ecuación de una recta tangente Paso 4

4. También puede ser necesario convertir esta ecuación a otra forma para obtener la respuesta final, si las instrucciones que acompañan al problema así lo requieren.