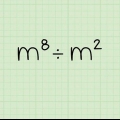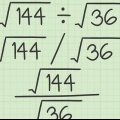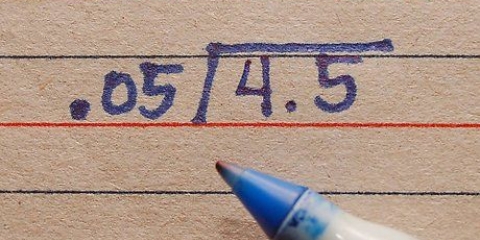Por ejemplo: la fracción  puedes simplificar a
puedes simplificar a  . Entonces,
. Entonces, 

Por ejemplo: porque  , ¿Puedes reescribir la expresión exponencial como
, ¿Puedes reescribir la expresión exponencial como  .
. 
Por ejemplo:  .
. 
Por ejemplo: porque ![Resolución de exponentes decimales 81^{{{frac{1}{4}}}}={raíz cuadrada[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b37415d73d383d0450962dda1cf0ddb2e0da0452) , puedes reescribir la ecuacion como
, puedes reescribir la ecuacion como ![Resolución de exponentes decimales ({sqrt[ {4}]{81}})^{{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a4e12743be369be81296fe2aeabd97c70cb9ab) .
. 
Por ejemplo: om ![Resolución de exponentes decimales {raíz cuadrada[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44f5722ccf46fec0200534e84bda483bc2b726b1) para calcular, necesitas determinar qué número multiplicado por cuatro es igual a 81. Porque
para calcular, necesitas determinar qué número multiplicado por cuatro es igual a 81. Porque  , Lo sabías
, Lo sabías ![Resolución de exponentes decimales {raíz cuadrada[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d91764f62522cec7024ef6481f0b83305f17e9) . Entonces la ecuación exponencial ahora se convierte en
. Entonces la ecuación exponencial ahora se convierte en  .
. 
Por ejemplo:  . Entonces,
. Entonces,  .
. 

el decimal  es igual a
es igual a  , Entonces
, Entonces  .
. 
Porque  se simplifica a
se simplifica a  , Eso cuenta
, Eso cuenta  .
. Si conviertes esto a una fracción impropia, obtienes  . Entonces,
. Entonces,  .
. 






Por ejemplo:  .
. 
Por ejemplo:  .
. 
![Resolución de exponentes decimales x^{{{frac{1}{3}}}}={raíz cuadrada[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
![Resolución de exponentes decimales x^{{{frac{1}{4}}}}={raíz cuadrada[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/625ea5fe7631555b2fc23ac21f595d7c20633ec9)
![Resolución de exponentes decimales x^{{{frac{1}{5}}}}={raíz cuadrada[ {5}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/788c8c448ea3cf9b81867b10ba6bbb1a47abb388)
Por ejemplo: ![Resolución de exponentes decimales 81^{{{frac{1}{4}}}}={raíz cuadrada[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/0af496f05893da79ec2c45b4ebebabce0930dce0) . Sabes que tres es la raíz cuarta de 81 porque
. Sabes que tres es la raíz cuarta de 81 porque 

Si se trata de exponentes de raíces cuadradas, entonces esta ley se convierte en  , porque
, porque  .
.
Resolución de exponentes decimales
Contenido
Calcular exponentes es una habilidad básica que los estudiantes aprenden en preálgebra. Por lo general, ves los exponentes como números enteros y, a veces, los ves como fracciones. Rara vez los ves como decimales. Cuando un exponente se muestra como un decimal, debe convertir el decimal a una fracción. A continuación, hay algunas reglas y leyes con respecto a los exponentes que puedes usar para calcular la expresión.
Pasos
Parte 1 de 3: calcular un exponente decimal

1. Convertir el decimal a una fracción. Para convertir un decimal a una fracción, debes considerar el valor posicional. El denominador de la fracción es el valor posicional. Los dígitos del punto decimal son iguales al numerador.
- Por ejemplo: para la expresión exponencial
, tienes que
convertir a una fracción. Como el decimal va al lugar de las centésimas, la fracción correspondiente es
.

2. Simplifica la fracción, si es posible. Dado que está sacando una raíz que corresponde al denominador de la fracción del exponente, desea que el denominador sea lo más pequeño posible. Hacer esto simplificación del descanso. Si la fracción es un número mixto (d.w.z. si su exponente es un decimal mayor que 1), reescríbalo como una fracción impropia.
 puedes simplificar a
puedes simplificar a  . Entonces,
. Entonces, 

3. Reescribe el exponente como una multiplicación. Para hacer esto, haga que el numerador sea un número entero y multiplíquelo por la fracción raíz. La raíz de fracción es la fracción con el mismo denominador, pero con 1 como numerador.
 , ¿Puedes reescribir la expresión exponencial como
, ¿Puedes reescribir la expresión exponencial como  .
.
4. Reescribe el exponente como una potencia de una potencia. Recuerda que multiplicar dos exponentes es lo mismo que la potencia de una potencia. Entonces  se convierte
se convierte  .
.
 se convierte
se convierte  .
. .
.
5. Reescribir la base como una ecuación de raíz cuadrada. Calcular el exponente de un número es equivalente a calcular una raíz adecuada de ese número. Entonces reescribe la base y el primer exponente como una ecuación de raíz cuadrada.
![Resolución de exponentes decimales 81^{{{frac{1}{4}}}}={raíz cuadrada[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b37415d73d383d0450962dda1cf0ddb2e0da0452) , puedes reescribir la ecuacion como
, puedes reescribir la ecuacion como ![Resolución de exponentes decimales ({sqrt[ {4}]{81}})^{{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a4e12743be369be81296fe2aeabd97c70cb9ab) .
.
6. Calcular la ecuación raíz cuadrada. Recuerda que el exponente de la raíz (el número pequeño fuera del radical) te dice qué raíz estás buscando. Si los números son complicados, es mejor hacer esto con el ![Resolución de exponentes decimales {raíz cuadrada[ {x}]{y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c28156258e3c4cf15e8af14abcc0163150e3e6) funcion en una calculadora matematica.
funcion en una calculadora matematica.
![Resolución de exponentes decimales {raíz cuadrada[ {x}]{y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c28156258e3c4cf15e8af14abcc0163150e3e6) funcion en una calculadora matematica.
funcion en una calculadora matematica.![Resolución de exponentes decimales {raíz cuadrada[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44f5722ccf46fec0200534e84bda483bc2b726b1) para calcular, necesitas determinar qué número multiplicado por cuatro es igual a 81. Porque
para calcular, necesitas determinar qué número multiplicado por cuatro es igual a 81. Porque  , Lo sabías
, Lo sabías ![Resolución de exponentes decimales {raíz cuadrada[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d91764f62522cec7024ef6481f0b83305f17e9) . Entonces la ecuación exponencial ahora se convierte en
. Entonces la ecuación exponencial ahora se convierte en  .
.
7. Calcular el exponente restante. Ahora debería tener un número entero como exponente, por lo que el cálculo debería ser simple de lo contrario. Siempre puedes usar una calculadora si los números son demasiado grandes.
 . Entonces,
. Entonces,  .
.Parte 2 de 3: Resolver un problema de muestra

1. Calcula la siguiente ecuación exponencial: .
.
 .
.
2. Convertir el decimal a una fracción. Porque  es mayor que 1, la fracción es un número mixto.
es mayor que 1, la fracción es un número mixto.
 es mayor que 1, la fracción es un número mixto.
es mayor que 1, la fracción es un número mixto. es igual a
es igual a  , Entonces
, Entonces  .
.
3. Simplifica la fracción, si es posible. También debes convertir cualquier número mixto a fracciones impropias.
 se simplifica a
se simplifica a  , Eso cuenta
, Eso cuenta  .
. . Entonces,
. Entonces,  .
.
4. Reescribe el exponente como una multiplicación. Porque  , puedes reescribir la ecuacion como
, puedes reescribir la ecuacion como  .
.
 , puedes reescribir la ecuacion como
, puedes reescribir la ecuacion como  .
.
5. Reescribe el exponente como una potencia de una potencia. Entonces,  .
.
 .
.
6. Reescribir la base como una ecuación de raíz cuadrada.![Resolución de exponentes decimales 256^{{{frac{1}{4}}}}={raíz cuadrada[ {4}]{256}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9c02c237d2aeb16bc1fd12eaf89cbde1d683a4) , lo que le permite reescribir la ecuación como
, lo que le permite reescribir la ecuación como ![Resolución de exponentes decimales ({sqrt[ {4}]{256}})^{{9}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261990049bf6155622a73330e280af3d17084588) .
.
![Resolución de exponentes decimales 256^{{{frac{1}{4}}}}={raíz cuadrada[ {4}]{256}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9c02c237d2aeb16bc1fd12eaf89cbde1d683a4) , lo que le permite reescribir la ecuación como
, lo que le permite reescribir la ecuación como ![Resolución de exponentes decimales ({sqrt[ {4}]{256}})^{{9}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261990049bf6155622a73330e280af3d17084588) .
.
7. Calcular la ecuación raíz cuadrada.![Resolución de exponentes decimales {raíz cuadrada[ {4}]{256}}=4](https://wikimedia.org/api/rest_v1/media/math/render/svg/55bb3e8f3f86ce5c35d5f18ddd8f486e75e67476) . Entonces la ecuación es ahora
. Entonces la ecuación es ahora  .
.
![Resolución de exponentes decimales {raíz cuadrada[ {4}]{256}}=4](https://wikimedia.org/api/rest_v1/media/math/render/svg/55bb3e8f3f86ce5c35d5f18ddd8f486e75e67476) . Entonces la ecuación es ahora
. Entonces la ecuación es ahora  .
.
8. Calcular el exponente restante. . Entonces,
. Entonces,  .
.
 . Entonces,
. Entonces,  .
.Parte 3 de 3: comprender los exponentes

1. Reconocer una ecuación exponencial. Una ecuación exponencial tiene una base y un exponente. La base es el número mayor en la ecuación. el exponente es el numero mas pequeño.
- Por ejemplo: en la ecuación
, es
la base y
el exponente.

2. Reconocer las partes de una ecuación exponencial. la base es el numero que se multiplica. El exponente indica con qué frecuencia se usa la base como factor en la ecuación.
 .
.
3. Reconocer un exponente de raíz cuadrada. Un exponente de raíz cuadrada también se puede llamar exponente de fracción. Es un exponente en forma de fracción.
 .
.
4. Comprender la relación entre raíz cuadrada y exponentes de raíz cuadrada. la exaltación  de un número es como la raíz cuadrada de ese número. Entonces,
de un número es como la raíz cuadrada de ese número. Entonces,  . Lo mismo ocurre con otras raíces y exponentes. El denominador del exponente te dice qué raíz sacar:
. Lo mismo ocurre con otras raíces y exponentes. El denominador del exponente te dice qué raíz sacar:
 de un número es como la raíz cuadrada de ese número. Entonces,
de un número es como la raíz cuadrada de ese número. Entonces,  . Lo mismo ocurre con otras raíces y exponentes. El denominador del exponente te dice qué raíz sacar:
. Lo mismo ocurre con otras raíces y exponentes. El denominador del exponente te dice qué raíz sacar:![Resolución de exponentes decimales x^{{{frac{1}{3}}}}={raíz cuadrada[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
![Resolución de exponentes decimales x^{{{frac{1}{4}}}}={raíz cuadrada[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/625ea5fe7631555b2fc23ac21f595d7c20633ec9)
![Resolución de exponentes decimales x^{{{frac{1}{5}}}}={raíz cuadrada[ {5}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/788c8c448ea3cf9b81867b10ba6bbb1a47abb388)
![Resolución de exponentes decimales 81^{{{frac{1}{4}}}}={raíz cuadrada[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/0af496f05893da79ec2c45b4ebebabce0930dce0) . Sabes que tres es la raíz cuarta de 81 porque
. Sabes que tres es la raíz cuarta de 81 porque 

5. Comprender la ley exponencial de la potencia de una potencia. Esta ley establece que  . En otras palabras, elevar un exponente a la potencia es lo mismo que multiplicar dos exponentes.
. En otras palabras, elevar un exponente a la potencia es lo mismo que multiplicar dos exponentes.
 . En otras palabras, elevar un exponente a la potencia es lo mismo que multiplicar dos exponentes.
. En otras palabras, elevar un exponente a la potencia es lo mismo que multiplicar dos exponentes. , porque
, porque  .
.Artículos sobre el tema. "Resolución de exponentes decimales"
Оцените, пожалуйста статью
Similar
Popular