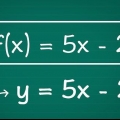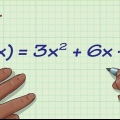se está convirtiendo
se está convirtiendo 
 se está convirtiendo
se está convirtiendo 
 se está convirtiendo
se está convirtiendo  .
.








Si los dos resultados son iguales, entonces f(x)=f(-x), y la función original es par. Un ejemplo es:  y
y  .
.Estos dos son iguales, por lo que la función es uniforme. Si cada término de la nueva versión de la función es el recíproco del término correspondiente de la original, entonces f(x)=-f(-x) y la función es impar. Por ejemplo:  pero
pero  .
.Tenga en cuenta que si multiplica cada término de la primera función por -1, hace que la segunda función. Entonces la función original g(x) es impar. Si la nueva función no coincide con ninguno de estos dos ejemplos, entonces no es ni par ni impar. Por ejemplo:  pero
pero  . El primer término es el mismo en todas las funciones, pero el segundo término es un inverso. Por lo tanto, esta función no es ni par ni impar.
. El primer término es el mismo en todas las funciones, pero el segundo término es un inverso. Por lo tanto, esta función no es ni par ni impar.

Puede probar la simetría seleccionando puntos individuales. Si el valor de y de cualquier valor de x es el mismo que el valor de y de -x, entonces la función es par. Los puntos elegidos arriba para trazar  dar los siguientes resultados:
dar los siguientes resultados: (1.3) y (-1.3) (2.9) y (-2.9). Los valores de y correspondientes para x=1 y x=-1, y para x=2 y x=-2, indican que esta es una función par. Para una mejor prueba, seleccionar dos puntos no es evidencia suficiente, pero es una buena indicación. 
Si elige un par de valores de prueba para x y sus valores correspondientes inversos para -x, debería obtener resultados inversos. Considere la función  . Esta función devuelve los siguientes puntos:
. Esta función devuelve los siguientes puntos:  . El punto es (1,2).
. El punto es (1,2). . El punto es (-1,-2).
. El punto es (-1,-2). . El punto es (2,10).
. El punto es (2,10). . El punto es (-2,-10).
. El punto es (-2,-10).Entonces f(x)=-f(-x), y puedes concluir que la función es impar. 
Elija un par de valores para x y -x, de la siguiente manera:  . El punto a trazar es (1,4).
. El punto a trazar es (1,4). . El punto a graficar es (-1,-2).
. El punto a graficar es (-1,-2). . El punto a trazar es (2,10).
. El punto a trazar es (2,10). . El punto a trazar es (2,-2).
. El punto a trazar es (2,-2).Esto ya te da suficientes puntos para notar que no hay simetría. Los valores de y para pares opuestos de valores de x no son iguales, ni son inversos entre sí. Esta función no es ni par ni impar. Es posible que vea esta característica,  , se puede reescribir como
, se puede reescribir como  . Escrito de esta forma, parece que es una función par porque solo hay un exponente, y ese es un número par. Sin embargo, este ejemplo ilustra que no puede determinar si una función es par o impar cuando está encerrada entre paréntesis. Tienes que evaluar la función en términos individuales y luego examinar los exponentes.
. Escrito de esta forma, parece que es una función par porque solo hay un exponente, y ese es un número par. Sin embargo, este ejemplo ilustra que no puede determinar si una función es par o impar cuando está encerrada entre paréntesis. Tienes que evaluar la función en términos individuales y luego examinar los exponentes.
Saber si una función es par o impar
Contenido
Una forma de clasificar las funciones es `par`, `impar` o ninguna. Estos términos se refieren a la repetición o simetría de la función. La mejor manera de averiguarlo es manipulando algebraicamente la función. También puedes estudiar la gráfica de la función y buscar simetría. Una vez que sepa cómo clasificar las características, también podrá predecir la apariencia de ciertas combinaciones de características.
Pasos
Método 1 de 2: probar la función algebraicamente

1. Ver variables inversas. En álgebra, el recíproco de una variable es negativo. Esto es cierto o la variable de la función ahora  es o algo mas. Si la variable de la función original ya es negativa (o una resta), entonces su recíproco es positivo (o una suma). Los siguientes son algunos ejemplos de variables y sus inversas:
es o algo mas. Si la variable de la función original ya es negativa (o una resta), entonces su recíproco es positivo (o una suma). Los siguientes son algunos ejemplos de variables y sus inversas:
 es o algo mas. Si la variable de la función original ya es negativa (o una resta), entonces su recíproco es positivo (o una suma). Los siguientes son algunos ejemplos de variables y sus inversas:
es o algo mas. Si la variable de la función original ya es negativa (o una resta), entonces su recíproco es positivo (o una suma). Los siguientes son algunos ejemplos de variables y sus inversas: - el inverso de
es
- el inverso de
es
- el inverso de
es
.

2. Reemplazar cada variable de la función con su inversa. No cambies la función original excepto el carácter. Por ejemplo:
 se está convirtiendo
se está convirtiendo 
 se está convirtiendo
se está convirtiendo 
 se está convirtiendo
se está convirtiendo  .
.
3. Simplificar la nueva característica. En este punto no tienes que preocuparte por resolver la función para un valor numérico dado. Simplemente simplifica las variables para comparar la nueva función, f(-x), con la función original, f(x). Recuerda las reglas básicas de los exponentes que dicen que una base negativa a una potencia par será positiva, mientras que una base negativa a una potencia impar será negativa.








4. Compara las dos funciones. Para cada ejemplo que pruebe, compare la versión simplificada de f(-x) con la f(x) original. Coloque los términos uno al lado del otro para facilitar la comparación y compare los signos de todos los términos.
 y
y  .
. pero
pero  .
. pero
pero  . El primer término es el mismo en todas las funciones, pero el segundo término es un inverso. Por lo tanto, esta función no es ni par ni impar.
. El primer término es el mismo en todas las funciones, pero el segundo término es un inverso. Por lo tanto, esta función no es ni par ni impar.Método 2 de 2: Pruebe la función gráficamente

1. Graficar la función. Use papel cuadriculado o una calculadora gráfica para graficar la función. Elija diferentes valores numéricos para  y conéctelo a la función para obtener el valor resultante de
y conéctelo a la función para obtener el valor resultante de  calcular. Trace estos puntos en el gráfico y después de trazar varios puntos, dibuje una línea a través de ellos para graficar la función.
calcular. Trace estos puntos en el gráfico y después de trazar varios puntos, dibuje una línea a través de ellos para graficar la función.
 y conéctelo a la función para obtener el valor resultante de
y conéctelo a la función para obtener el valor resultante de  calcular. Trace estos puntos en el gráfico y después de trazar varios puntos, dibuje una línea a través de ellos para graficar la función.
calcular. Trace estos puntos en el gráfico y después de trazar varios puntos, dibuje una línea a través de ellos para graficar la función. - Al trazar los puntos, preste atención a los valores negativos positivos y correspondientes para
. Por ejemplo, si se trata de la función
, luego trazas los siguientes valores:
. Esto da como resultado el punto
.
. Esto da como resultado el punto
.
. Esto da como resultado el punto
.
. Esto da como resultado el punto
.

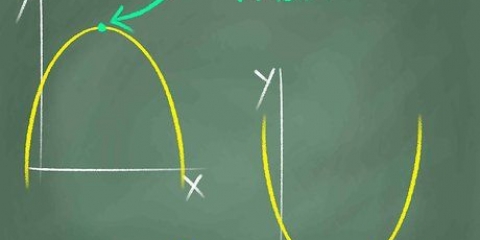
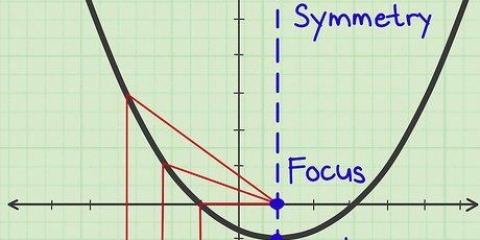
2. Tenga en cuenta la simetría a lo largo del eje y. Al observar una función, la simetría sugerirá una imagen especular. Si ve que la parte del gráfico en el lado derecho (positivo) del eje y coincide con la parte del gráfico en el lado izquierdo (negativo) del eje y, entonces el gráfico es simétrico con respecto al eje y. Si una función es simétrica con respecto al eje y, entonces la función es par.
 dar los siguientes resultados:
dar los siguientes resultados:
3. Prueba de simetría desde el origen. El origen es el punto central (0,0). La simetría de origen significa que un resultado positivo para un valor de x elegido corresponderá a un resultado negativo para -x, y viceversa. Las funciones impares exhiben simetría de origen.
 . Esta función devuelve los siguientes puntos:
. Esta función devuelve los siguientes puntos: . El punto es (1,2).
. El punto es (1,2). . El punto es (-1,-2).
. El punto es (-1,-2). . El punto es (2,10).
. El punto es (2,10). . El punto es (-2,-10).
. El punto es (-2,-10).
4. Mira si no hay simetría. El último ejemplo es una función sin simetría en ambos lados. Si observa el gráfico, verá que no es una imagen especular ni en el eje y ni alrededor del origen. Ver la función  .
.
 .
. . El punto a trazar es (1,4).
. El punto a trazar es (1,4). . El punto a graficar es (-1,-2).
. El punto a graficar es (-1,-2). . El punto a trazar es (2,10).
. El punto a trazar es (2,10). . El punto a trazar es (2,-2).
. El punto a trazar es (2,-2). , se puede reescribir como
, se puede reescribir como  . Escrito de esta forma, parece que es una función par porque solo hay un exponente, y ese es un número par. Sin embargo, este ejemplo ilustra que no puede determinar si una función es par o impar cuando está encerrada entre paréntesis. Tienes que evaluar la función en términos individuales y luego examinar los exponentes.
. Escrito de esta forma, parece que es una función par porque solo hay un exponente, y ese es un número par. Sin embargo, este ejemplo ilustra que no puede determinar si una función es par o impar cuando está encerrada entre paréntesis. Tienes que evaluar la función en términos individuales y luego examinar los exponentes.Consejos
- Si todas las formas de una variable en la función tienen exponentes pares, entonces la función es par. Si todos los exponentes son impares, entonces la función es impar en general.
Advertencia
- Este artículo solo se aplica a funciones con dos variables, que se pueden representar gráficamente en un sistema de coordenadas bidimensional.
Artículos sobre el tema. "Saber si una función es par o impar"
Оцените, пожалуйста статью
Similar
Popular