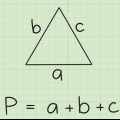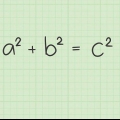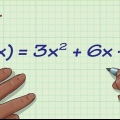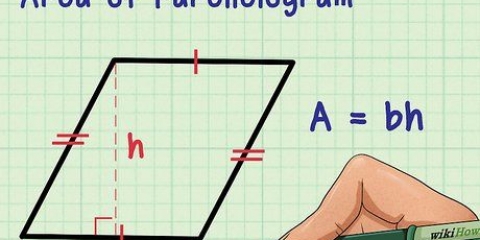Determinar el tercer ángulo de un triángulo

Contenido

Pasos
Advertencias

Determinar el tercer ángulo de un triángulo si sabes cuáles son los otros dos ángulos es fácil. Todo lo que tienes que hacer es restar los otros ángulos de 180° para encontrar el tercer ángulo. Sin embargo, hay algunas otras formas de determinar el tercer ángulo de un triángulo, dependiendo del problema con el que estés trabajando. Si desea saber cómo determinar esa ilustre tercera esquina de un triángulo, lea el Paso 1 para comenzar.

Pasos

Método 1 de 3: usar las otras dos esquinas

Imagen titulada Encuentra el tercer ángulo de un triángulo Paso 1

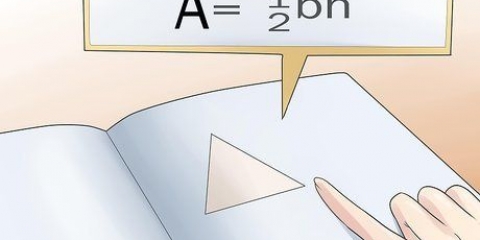
1. Suma los dos ángulos conocidos. Todo lo que necesitas saber es que todos los ángulos de un triángulo suman siempre ser 180°. esto siempre es verdad. Entonces, si conoces dos de las tres esquinas del triángulo, solo te falta una pequeña pieza del rompecabezas. Lo primero que puedes hacer es sumar los ángulos que ya conoces. En este ejemplo, los ángulos que conoces son 80° y 65°. Súmalos (80° + 65°) para obtener 145°.

Imagen titulada Encuentra el tercer ángulo de un triángulo Paso 2

2. Resta este número de 180°. los angulos de un triangulo se suman 180°. Por lo tanto deber el ángulo restante junto con los otros ángulos son 180°. En este ejemplo: 180° - 145° = 35°.

Imagen titulada Encuentra el tercer ángulo de un triángulo Paso 3

3. Escribe tu respuesta. Ahora sabes que el tercer ángulo es de 35°. En caso de duda, simplemente verifique su trabajo. Los tres ángulos juntos deben ser de 180° grados, de lo contrario no es un triángulo. 80° + 65° + 35° = 180°. Ya está todo listo.

Método 2 de 3: usar variables

Imagen titulada Encuentra el tercer ángulo de un triángulo Paso 4

1. Escribe el problema. A veces no tienes tanta suerte y no sabes los valores de los dos ángulos de un triángulo, pero solo tienes unas pocas variables, o unas pocas variables y un ángulo. Digamos que estás lidiando con el siguiente problema: Determinar el ángulo `x` del triángulo de dimensiones `x`, `2x` y 24°. Solo escribe esto primero.

Imagen titulada Encuentra el tercer ángulo de un triángulo Paso 5

2. Sume todas las dimensiones juntas. Es el mismo principio que seguirías si conocieras los dos ángulos. Simplemente haga coincidir los valores de los ángulos combinando las variables. Entonces, x + 2x + 24° = 3x + 24°.

Imagen titulada Encuentra el tercer ángulo de un triángulo Paso 6

3. Resta estos valores de 180°. Luego resta estos valores de 180° para acercarte a la solución del problema. Asegúrate de que la ecuación sea igual a 0. Esto es lo que parece:

180° - (3x + 24°) = 0

180° - 3x - 24° = 0

156° - 3x = 0

Imagen titulada Encuentra el tercer ángulo de un triángulo Paso 7

4. Ahora resuelve para x. Ahora mueve las variables a un lado de la ecuación y los números al otro lado. Obtienes 156° = 3x. Ahora divide ambos lados de la ecuación por 3 para obtener x = 52°. Esto significa que el tercer ángulo del triángulo debe ser de 52°. El otro ángulo es 2x (2x 52° o 104°).

Imagen titulada Encuentra el tercer ángulo de un triángulo Paso 8

5. Revisa tu trabajo. Si quieres asegurarte de que este es un triángulo válido, solo suma los tres valores de los ángulos para ver si suman 180°. Eso es 52° + 104° + 24° = 180°. Ya está todo listo.

Método 3 de 3: usar otros métodos

Imagen titulada Encuentra el tercer ángulo de un triángulo Paso 9

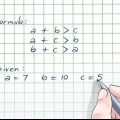
1. Hallar el tercer ángulo de un triángulo isósceles. Los triángulos isósceles tienen dos lados iguales y dos ángulos iguales. Cada uno de los lados iguales está marcado con un signo de almohadilla, lo que indica que los ángulos opuestos a ambos lados son iguales. Si conoces la medida angular de un ángulo igual de un triángulo isósceles, entonces también conoces el otro ángulo igual. Puede determinar esto de la siguiente manera:

Si uno de los ángulos iguales mide 40°, entonces sabes que el otro ángulo también mide 40°. Puedes encontrar el tercer lado, si es necesario, restando 40° + 40° (eso es 80°) de 180°. 180° - 80° = 100°, que es el ángulo restante.

Imagen titulada Encuentra el tercer ángulo de un triángulo Paso 10

2. Hallar el tercer ángulo de un triángulo equilátero. Un triángulo equilátero solo tiene lados iguales y ángulos iguales. A menudo, esto se indica mediante dos marcas en el medio de cada uno de los lados. Esto significa que el valor de cualquier ángulo en un triángulo equilátero es de 60°. Revisa tu trabajo. 60° + 60° + 60° = 180°.

Imagen titulada Encuentra el tercer ángulo de un triángulo Paso 11

3. Encuentra el tercer ángulo de un triángulo rectángulo. Suponga que tiene un triángulo rectángulo, cuyos otros ángulos son 30 °. Si es un triángulo rectángulo, entonces sabes que uno de los ángulos mide exactamente 90°. Se aplican los mismos principios. Todo lo que tienes que hacer es sumar los ángulos que conoces (30° + 90° = 120°) y restar ese número de 180°. Efectivamente, 180° - 120° = 60°. entonces el tercer angulo es 60°.

Advertencias

Cometer un error al sumar y restar deberá dar como resultado una respuesta incorrecta. Siempre es una buena idea revisar tu trabajo, incluso si no parece estar mal.