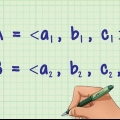Encuentra el ángulo entre dos vectores

Contenido

Pasos
Consejos

Los matemáticos y los físicos a menudo tienen que encontrar el ángulo entre dos vectores dados. Si bien es fácil encontrar el ángulo entre dos vectores en el mismo plano graficando, puede ser un poco más complicado en el espacio o en tres dimensiones. Este artículo explica el método a usar para encontrar el ángulo entre dos vectores en el plano o en el espacio.

Pasos

Método 1 de 4: determinar los vectores

1. Determina los vectores que necesitas para encontrar el ángulo. Toma los dos vectores A y OQ que se intersecan en el punto O, y calcula el ángulo MOQ. Debes usar los vectores A y OQ usar, no mes o QO. En caso de que mes es conocido, multiplícalo por -1 para obtener A Llegar.

Método 2 de 4: encontrar el producto escalar

Encuentre el producto escalar (o producto escalar) de los dos vectores. Si no sabes cómo calcular el producto escalar de dos vectores, sigue leyendo:

1. Determinar las componentes del vector en cada dirección. Cuando los vectores se enumeran en una tabla, la primera fila generalmente representa el eje x, la segunda fila representa el eje y y la tercera representa el eje z. Si el vector se escribe en la forma xI + yj + zk, luego establezca los coeficientes de yo, y k la magnitud de los componentes a lo largo de los ejes x, y y z (yo, y k son los vectores a lo largo de los ejes x, y y z).

2. Multiplica las componentes de ambos vectores a lo largo del eje x. Luego multiplique las componentes de ambos vectores a lo largo del eje y y haga lo mismo con las componentes a lo largo del eje z.

3. Suma los tres productos juntos. Este es el producto escalar de ambos vectores. El producto escalar, o "producto interno", de dos vectores es un número muy útil en geometría y física. Por el momento solo usamos este producto como herramienta para calcular el ángulo entre dos vectores. En un vector bidimensional, el componente a lo largo del eje z es cero, por lo que el producto escalar se puede encontrar considerando solo los componentes a lo largo del eje x e y.

Método 3 de 4: calcular el tamaño

1. Calcular la magnitud de los dos vectores. Calcular la magnitud de los dos vectores, usando la fórmula a=b+c+d, por lo cual a es la magnitud del vector, y antes de Cristo, y D el tamaño de los componentes en las tres direcciones diferentes. en el plano D ser igual a cero.