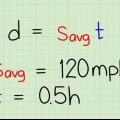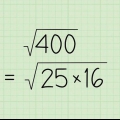Cómo calcular la distancia entre dos puntos: 6 pasos (con fotos)

Contenido

Pasos
Consejos

Piense en la distancia entre dos puntos como una línea. La longitud de esta línea se puede encontrar usando la fórmula de la distancia: $\sqrt{(} (X_{2} - X_{1})^{2} + (y_{2} - y_{1})^{2})$ ${sqrt(}(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})$ .

Pasos

Imagen titulada Encuentra la distancia entre dos puntos Paso 2

1. Toma las coordenadas de dos puntos entre los que quieres encontrar la distancia. Llama a un punto 1 (x1,y1) y al otro punto 2 (x2,y2). No importa desde qué punto comiences, siempre que apliques las etiquetas (1 y 2) de manera consistente a lo largo del problema.

x1 es la coordenada horizontal (a lo largo del eje x) del punto 1, y x2 es la coordenada horizontal del punto 2. y1 es la coordenada vertical (a lo largo del eje y) del punto 1, y y2 es la coordenada vertical del punto 2.
No, por ejemplo los puntos (3.2) y (7.8). Si (3.2) es igual a (x1,y1), entonces (7.8) es igual a (x2,y2).

Imagen titulada Encuentra la distancia entre dos puntos Paso 1

2. Usa la fórmula de la distancia. Esta fórmula determina la longitud de una línea recta entre dos puntos: el punto 1 y el punto 2. La distancia lineal es la raíz cuadrada del cuadrado de la distancia horizontal más el cuadrado de la distancia vertical entre dos puntos. En pocas palabras, es la raíz cuadrada de:

(X 2 - X_{1})^{2} + (y_{2} - y_{1})^{2}

$(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}$

Imagen titulada Encuentra la distancia entre dos puntos Paso 3

3. Determine la distancia horizontal y vertical entre los puntos. Primero calcule y2 - y1 para encontrar la distancia vertical. Luego calcula x2 - x1 para encontrar la distancia horizontal. No te preocupes si la resta produce números negativos. El siguiente paso es elevar al cuadrado estos valores (que siempre da como resultado un entero positivo).

Determine la distancia a lo largo del eje y. Para los puntos de ejemplo (3.2) y (7.8), donde el punto 1 es (3.2) y el punto 2 (7.8) esto se convierte en: (y2 - y1) = 8 - 2 = 6. Esto significa que la distancia en el eje y entre estos dos puntos es de seis unidades de longitud.

Determine la distancia a lo largo del eje x. Para los mismos puntos muestrales (3.2) y (7.8): (x2 - x1) = 7 - 3 = 4. Esto significa que hay cuatro unidades de longitud que separan los dos puntos en el eje x.

Imagen titulada Encuentra la distancia entre dos puntos Paso 4

4. Elevar al cuadrado ambos valores. Esto significa que elevas al cuadrado la distancia del eje x (x2 - x1), y elevas al cuadrado la distancia del eje y (y2 - y1).

62 = 36

$6^{2}=36$

42 = dieciséis

$4^{2}=16$

Imagen titulada Encuentra la distancia entre dos puntos Paso 5

5. Suma los cuadrados juntos. Esto le dará el cuadrado de la distancia diagonal, lineal entre sus dos puntos. En el ejemplo de los puntos (3.2) y (7.8) el cuadrado de (7 - 3) es 16, y el cuadrado de (8 - 2) es 36. 36 + 16 = 52.

Imagen titulada Encuentra la distancia entre dos puntos Paso 6

6. Saca la raíz cuadrada de la ecuación. Este es el último paso en la ecuación. La distancia lineal entre los dos puntos es la raíz cuadrada de la suma de los cuadrados de la distancia en el eje x y la distancia en el eje y.

Siguiendo con el ejemplo, la distancia entre (3.2) y (7.8) es la raíz cuadrada de 52, o aproximadamente 7.21.

Consejos

No importa si obtienes un número negativo después de restar y2 - y1 o x2 - x1. Debido a que la diferencia está al cuadrado, siempre obtienes una distancia positiva en tu respuesta.