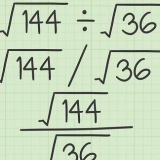Cómo determinar la precisión

Contenido

Pasos
Consejos

Precisión significa que una medición con una herramienta o instrumento en particular produce resultados similares cada vez que se usa. Por ejemplo, si se sube a una báscula cinco veces seguidas, una báscula precisa debería mostrarle el mismo peso cada vez. En matemáticas y ciencias, la precisión de cálculo es esencial para determinar si sus instrumentos y medidas son lo suficientemente buenos para obtener buenos datos. Puede representar la precisión de cada conjunto de datos usando el rango de los valores, la desviación media o la desviación estándar.

Pasos

Método 1 de 4: Cálculo del rango

Imagen titulada Calculate Precision Step 1

1. Determinar el valor medido más alto. Es útil comenzar a clasificar sus datos en orden numérico, de menor a mayor. Esto asegurará que no se salte ninguno de los valores. Luego seleccione el valor al final de la lista.

Por ejemplo, supongamos que prueba la precisión de una escala y ve cinco lecturas: 11, 13, 12, 14, 12. Ordenados estos valores se muestran como 11, 12, 12, 13, 14. El valor más alto es 14.

Imagen titulada Calculate Precision Step 2

2. Determinar el valor medido más bajo. Una vez ordenados sus datos, encontrar el valor más bajo es tan simple como mirar el principio de la lista.

Dentro de los datos de medición de la escala, el valor más bajo es 11.

Imagen titulada Calculate Precision Step 3

3. Reste el valor más bajo del más alto. El rango de un conjunto de datos es la diferencia entre las lecturas más alta y más baja. Solo resta el uno del otro. Algebraicamente, el rango se expresa como:

rango = X (metro a X) - X (metro I norte)

${text{Rango}}=x(máx)-x(mín)$

El rango de los datos de la muestra es:

rango = X (metro a X) - X (metro I norte) = 14 - 11 = 3

${text{Rango}}=x(máximo)-x(mínimo)=14-11=3$

Imagen titulada Calculate Precision Step 4

4. Mostrar el rango como la precisión. Al informar datos, es importante que los lectores sepan lo que ha medido. Debido a que la precisión viene en diferentes métricas, debe especificar lo que desea informar. Para estos datos usted declara: media = 12.4, rango = 3. O simplemente: media = 12,4 ±3.

La media no es necesariamente una parte del cálculo del rango o la precisión, pero generalmente es el primer cálculo para informar el valor medido. La media se obtiene dividiendo la suma de los valores medidos por el número de elementos del grupo. La media de esta serie de datos es (11 + 13 + 12 + 14 + 12) / 5 = 12,4.

Método 2 de 4: Cálculo de la desviación media

Imagen titulada Calculate Precision Step 5

1. Primero determine el promedio de los datos. La desviación media es una medida más detallada de la precisión de un grupo de medidas o valores de un experimento. El primer paso para encontrar la desviación media es calcular la media de los valores medidos. La media es la suma de los valores dividida por el número de mediciones.

En este ejemplo, estamos usando los mismos datos de muestra que antes. Suponga que se han tomado cinco medidas, 11, 12, 13, 14 y 12. La media de estos valores es (11 + 13 + 12 + 14 + 12) / 5 = 12,4.

Imagen titulada Calculate Precision Step 6

2. Calcular la desviación absoluta de cada valor de la media. Para este cálculo de precisión, debe determinar qué tan cerca está cada valor de la media. Para hacer esto, resta la media de cada número. Para esta medida, no importa si el valor está por encima o por debajo de la media. Resta los números y solo usa el valor positivo del resultado. Esto también se conoce como el `valor absoluto`.

Algebraicamente, el valor absoluto se representa colocando dos barras verticales alrededor del cálculo. Como sigue:

Desviación absoluta = | X - m |

${text{Desviación absoluta}}=|x-mu |$

Este cálculo establece

X

$X$ para cada uno de los valores experimentales y

m

$mu$ para el promedio calculado.

En cuanto a los valores de la serie de datos muestrales, las desviaciones absolutas son:

| 12 - 12, 4 | = 0, 4

$|12-12,4|=0,4$

| 11 - 12, 4 | = 1, 4

$|11-12,4|=1,4$

| 14 - 12, 4 | = 1, 6

$|14-12,4|=1,6$

| 13 - 12, 4 | = 0, 6

$|13-12,4|=0,6$

| 12 - 12, 4 | = 0, 4

$|12-12,4|=0,4$

Imagen titulada Calculate Precision Step 7

3. Determinar la desviación media. Usa las desviaciones absolutas y encuentra su media. Al igual que con el conjunto original de datos, sumas los valores y divides la suma por la cantidad de valores. Esto se representa algebraicamente como:

Desviación media = Σ | X - m | norte

${text{Desviación media}}={frac{Sigma |x-mu |}{n}}$

En cuanto a estos datos de muestra, el cálculo es así:

Desviación media = 0, 4 + 1, 4 + 1, 6 + 0, 6 + 0, 4 5

${text{Desviación media}}={frac{0.4+1.4+1.6+0.6+0.4}{5}}$

Desviación media = 4, 4 5

${text{Desviación media}}={frac{4,4}{5}}$

Desviación media = 0, 88

${text{Desviación media}}=0,88$

Imagen titulada Calculate Precision Step 8

4. Indique el resultado de la precisión. Este resultado se puede informar como la media, más o menos la desviación media. Para este conjunto de datos de muestra, parece 12,4 ±0,88. Tenga en cuenta que establecer la precisión como la desviación media hace que la medición parezca mucho más precisa que con el rango.

Método 3 de 4: calcular la desviación estándar

Imagen titulada Calculate Precision Step 9

1. Use la fórmula correcta para la desviación estándar. Para cualquier tamaño de conjunto de datos, la desviación estándar es una estadística confiable para mostrar precisión. Hay dos fórmulas para calcular la desviación estándar, con una diferencia muy pequeña entre ellas. Utiliza una fórmula si sus métricas cubren una población completa. La segunda fórmula se usa si los datos medidos son solo una muestra de la población.

Sus datos representan una población completa si ha recopilado todas las medidas posibles de todos los sujetos posibles. Por ejemplo, si está evaluando a personas con una enfermedad muy rara y está seguro de que ha evaluado a todas las personas con esta enfermedad, esto incluye a toda la población. La fórmula para la desviación estándar en este caso es:

$Σ = \sqrt{} Σ (X - m) 2 norte$ $sigma ={sqrt{{frac{Sigma (x-mu)^{2}}{n}}}}$

Una muestra es un grupo de datos más pequeño que una población completa. Usualmente usarás este más. La fórmula de desviación estándar para una muestra es:

Σ = \sqrt{} Σ (X - m) 2 norte - 1

$sigma ={sqrt{{frac{Sigma (x-mu)^{2}}{n-1}}}}$

Tenga en cuenta que la única diferencia es el denominador de la fracción. Para una población completa, dividir por

norte

$norte$ . Si tienes una muestra, por favor comparte

norte - 1

$n-1$ .

Imagen titulada Calculate Precision Step 10

2. Encuentre el promedio de los valores de los datos. Al igual que con el cálculo de la desviación media, comienza determinando la media de los valores de los datos.

Usando el mismo conjunto de lecturas que se indicó anteriormente, la media es 12.4.

Imagen titulada Calculate Precision Step 11

3. Encuentra el cuadrado de cada variante. Para cada punto de datos, reste el valor de los datos de la media y eleve el resultado al cuadrado. Como estás elevando al cuadrado estas variaciones, no importa si la diferencia es positiva o negativa. el cuadrado de la diferencia siempre es positivo.

Para los cinco valores de datos en este ejemplo, estos cálculos son así:

(12 - 12, 4) 2 = (- 0, 4)^{2} = 0, dieciséis

$(12-12,4)^{2}=(-0,4)^{2}=0,16$

(11 - 12, 4) 2 = (- 1, 4)^{2} = 1, 96

$(11-12,4)^{2}=(-1,4)^{2}=1,96$

(14 - 12, 4) 2 = 1, 6^{2} = 2, 56

$(14-12,4)^{2}=1,6^{2}=2,56$

(13 - 12, 4) 2 = 0, 6^{2} = 0, 36

$(13-12,4)^{2}=0,6^{2}=0,36$

(12 - 12, 4) 2 = (- 0, 4)^{2} = 0, dieciséis

$(12-12,4)^{2}=(-0,4)^{2}=0,16$

Imagen titulada Calculate Precision Step 12

4. Calcular la suma de las diferencias al cuadrado. El numerador de la fracción en la desviación estándar es la suma de las diferencias al cuadrado entre los valores y la media. Puede determinar esta cantidad sumando los números del cálculo anterior.

Para el conjunto de datos de muestra, estos son:

0, dieciséis + 1, 96 + 2, 56 + 0, 36 + 0, dieciséis = 5, 2

$0,16+1,96+2,56+0,36+0,16=5,2$

Imagen titulada Calculate Precision Step 13

5. Dividir por tamaño de datos. Este es el único paso que es diferente en un cálculo de población en comparación con una muestra. Para una población completa, se divide por

norte

$norte$ (el número de valores). En una muestra, se divide por

norte - 1

$n-1$ .

El siguiente ejemplo tiene solo cinco medidas y, por lo tanto, es solo una muestra. Entonces, para los cinco valores utilizados, divida por (5 - 1) o 4. El resultado es

5, 2 / 4 = 1, 3

$5,2/4=1,3$ .

Imagen titulada Calculate Precision Step 14

6. Encuentra la raíz cuadrada del resultado. En este punto, el cálculo representa lo que se llama la varianza del conjunto de datos. La desviación estándar es la raíz cuadrada de la varianza. Usa una calculadora para encontrar la raíz cuadrada, y con ella la desviación estándar.

Σ = \sqrt{1.3} = 1, 14

$sigma ={sqrt{1.3}}=1,14$

Imagen titulada Calculate Precision Step 15

7. Muestra tu resultado. Usando este cálculo, la precisión de la escala se puede indicar indicando la media más o menos la desviación estándar. Para este dato, se convierte en 12.4 ±1.14.

La desviación estándar es quizás la medida de precisión más común. Sin embargo, para mayor claridad, sigue siendo una buena idea usar una nota al pie o un paréntesis para indicar que el valor de precisión representa la desviación estándar.

Método 4 de 4: decide cómo declarar la precisión

Imagen titulada Calculate Precision Step 16

1. Usa correctamente la palabra exactitud. La precisión es un término utilizado para indicar la repetibilidad de las mediciones. Si está recolectando un grupo de datos, ya sea por medición o a través de un experimento en particular, la precisión describe qué tan cerca estarán los resultados de cada medición o experimento.

Precisión no es lo mismo que precisión. La precisión mide qué tan cerca están los valores experimentales del valor real o teórico, mientras que la precisión mide qué tan cerca están los valores medidos entre sí.
Los datos pueden ser exactos pero no exactos o exactos pero no exactos. Las lecturas precisas pueden estar cerca del objetivo, pero pueden no estar juntas. Las lecturas precisas están cerca unas de otras, estén o no cerca de los valores objetivo.

Imagen titulada Calculate Precision Step 17

2. Elija el mejor grado de precisión. La palabra `precisión` no tiene un solo significado. Es posible mostrar la precisión con múltiples medidas diferentes. Tendrás que decidir cuál es el mejor.

Rango. Para conjuntos de datos pequeños con aproximadamente diez o menos mediciones, el rango de valores es una buena medida de precisión. Esto es especialmente cierto si los valores se agrupan bastante juntos. Si encuentra que uno o dos valores están lejos de los otros valores, entonces probablemente debería usar un cálculo diferente.

Desviación media. La desviación media es una medida más precisa de la precisión de un pequeño conjunto de valores de datos.

Desviación Estándar. La desviación estándar es quizás la medida de precisión más reconocida. La desviación estándar se puede utilizar para calcular la precisión de las mediciones para una población completa o una muestra de la población.

Imagen titulada Calculate Precision Step 18

3. Proporcione una representación clara de sus resultados. Muy a menudo, los investigadores informarán los datos dando la media del valor medido seguido del grado de precisión. La precisión se muestra con el símbolo `±`. Esto da una indicación de precisión, pero no explica claramente al lector si el número después del símbolo `±` es un rango, una desviación estándar o alguna otra medida. Para indicar esto claramente, debe definir qué nivel de precisión ha utilizado, ya sea en una nota al pie o como un comentario entre paréntesis.

Para una serie de datos determinada, el resultado puede mostrarse como 12,4 ±3. Sin embargo, una forma más descriptiva de expresar los mismos datos sería esta: `Media = 12.4, Rango = 3.`

Consejos

Si uno de los valores de la muestra es mucho más alto o más bajo que el resto de sus valores, no excluya este valor de sus cálculos. Incluso si fue un error, sigue siendo un dato y debe usarse para el cálculo correcto.
Solo se usaron cinco valores en este artículo por simplicidad matemática. En un experimento real, debe usar más de cinco métricas para un cálculo más preciso. Cuantas más muestras ejecute, más preciso.