Calcular con vectores

Contenido

Pasos
Consejos

Los vectores son cantidades que constan de una magnitud y una dirección (por ejemplo: vector de velocidad o velocidad vectorial, aceleración y desplazamiento), a diferencia de los escalares, que solo tienen magnitud (como velocidad, distancia y energía). Mientras que los escalares se pueden sumar por sus tamaños (por ejemplo, 5 kJ + 6kJ = 11kJ), los vectores son un poco más complicados de calcular con. Consulte el Paso 1 a continuación para obtener más información sobre las formas de hacerlo.

Pasos

Método 1 de 3: sumar y restar vectores

Imagen titulada Suma o resta vectores Paso 1

1. Expresar las dimensiones de un vector usando notación vectorial. Debido a que los vectores tienen una magnitud y una dirección, por lo general es fácil descomponerlos en sus dimensiones x, y y/o z. Estas dimensiones generalmente se expresan en una notación equivalente a describir un punto en un sistema de coordenadas (por ejemplo,.

Tenga en cuenta que los vectores pueden ser de 1, 2 o 3 dimensiones. Entonces, los vectores pueden tener una componente x, una componente x e y, o una componente x, y, etc. Nuestro ejemplo a continuación es sobre vectores tridimensionales, pero el proceso es similar al del plano o una línea.

Supongamos que tenemos dos vectores tridimensionales, el vector A y el vector B. Podemos escribir estos vectores en notación vectorial como A =

Imagen titulada Suma o resta vectores Paso 2

2. Para sumar dos vectores, suma los componentes. Si se conocen las componentes de dos vectores, entonces es posible determinar los vectores sumando sus componentes correspondientes. En otras palabras, agregue la componente x del primer vector a la componente x del segundo y haga lo mismo para y y z. Las respuestas que obtiene al sumar los componentes x, y y z de los vectores originales son los componentes x, y y z del nuevo vector.

En palabras generales, A+B =

Sumemos los dos vectores A y B. un = <5, 9, -10> y B = <17, -3, -2>. A + B = <5+17, 9+-3, -10+-2>, o <22, 6, -12>.

Imagen titulada Suma o resta vectores Paso 3

3. Para restar dos vectores, restas sus componentes. Entonces lo mismo que con la adición, pero al revés.Si se conocen las componentes de dos vectores, restar un vector del otro no es más que restar las componentes.

En palabras generales, AB =

Restamos los dos vectores A y B. un = <18, 5, 3> y B = <-10, 9, -10>. A - B = <18--10, 5-9, 3--10>, o <28, -4, 13>.

Método 2 de 3: Suma y resta usando el método de la parte trasera

Imagen titulada Suma o resta vectores Paso 4

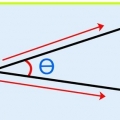
1. Indicar vectores con una flecha. Como los vectores tienen una magnitud y una dirección, puedes indicarlos con una flecha. En otras palabras, tienen un "punto de partida" y un "punto final", apuntando en la dirección del vector, con la magnitud del vector indicada por la flecha.

Al dibujar un vector a escala, debe medir los ángulos con cuidado. Los ángulos incorrectos darán como resultado una respuesta incorrecta con este método.

Imagen titulada Suma o resta vectores Paso 5

2. Dibujar las flechas en orden posterior. La punta de la flecha se coloca contra la cola de la siguiente flecha. Como solo está sumando dos vectores, esto es todo lo que necesita hacer para encontrar el vector resultante.

Tenga en cuenta que el orden en que dibuja los vectores no es importante, siempre que supongamos que siempre usa el mismo punto de partida. Vector A + Vector B = Vector B + Vector A

Imagen titulada Suma o resta vectores Paso 6

3. Para restar hacer el vector "negativo". Restar vectores con este método visual es relativamente fácil. Invierta la dirección del vector, pero mantenga el mismo tamaño y agréguelo usando el método de cabeza a cola como de costumbre. En otras palabras, para restar un vector, rotas el vector 180 y sumas.

Imagen titulada Suma o resta vectores Paso 7

4. Si desea sumar o restar más de dos vectores, vincule todos esos vectores uno tras otro usando el método de la parte trasera. No importa el orden. Puedes usar esto para cualquier número de vectores.

5. Dibuja un nuevo vector desde la cola del primer vector hasta la cabeza del último. Ya sea que esté trabajando con 2 o 100 vectores, el vector que se extiende desde el punto inicial (la cola de su primer vector) hasta el punto final de los vectores agregados (la cabeza de su último vector) es el resultado vector, o la suma de todos los vectores. Tenga en cuenta que este vector es igual al vector obtenido al sumar los componentes x, y y/o z de todos los vectores.

Imagen titulada Suma o resta vectores Paso 8

Como dibujó todos los vectores a escala y midió los ángulos exactamente, puede encontrar la magnitud del vector resultante midiendo la longitud. También puede medir el ángulo que forma esta resultante con un vector específico o con la horizontal/vertical, etc. para encontrar la dirección.

Como no ha dibujado todos los vectores a escala, probablemente tendrá que calcular la magnitud de la resultante usando trigonometría. Use la regla del seno o del coseno para esto. Dado que está sumando más de dos vectores, es útil sumar dos de ellos primero, luego sumar su resultante al tercer vector, y así sucesivamente. Mira la siguiente sección para mas información.

Imagen titulada Suma o resta vectores Paso 9

6. Mostrar el vector resultante por tamaño y dirección. Los vectores están determinados por su longitud y dirección. Como se indicó anteriormente, suponiendo que haya dibujado los vectores con precisión, la magnitud del vector es igual a su longitud y dirección, y su ángulo es relativo a la vertical, horizontal, etc. Usa las unidades de los vectores que sumaste para elegir las unidades para la magnitud del vector resultante.

Por ejemplo, si los vectores que agregamos representan un vector de velocidad en ms, entonces podríamos representar el vector resultante como "un vector de velocidad de X ms en y relativo a la horizontal".

Método 3 de 3: sumar y restar vectores determinando las componentes

Imagen titulada Suma o resta vectores Paso 10

1. Usa la trigonometría para encontrar los componentes del vector. Necesita la magnitud y la dirección en relación con la horizontal o la vertical, y necesita tener algún conocimiento práctico de trigonometría. Supongamos que tenemos un vector 2-D. Primero, conviertes los vectores en la hipotenusa de un triángulo rectángulo, con los otros dos lados paralelos a los ejes x e y. Puedes pensar en estos dos lados como vectores de la cabeza a la cola que, cuando se suman, producen el vector original.

Las longitudes de los dos lados son iguales a las magnitudes de los componentes x e y de su vector y se pueden calcular usando trigonometría. Si x es la magnitud del vector, entonces el lado adyacente al ángulo del vector (en relación con la horizontal, vertical, etc.) igual a xcos(θ), mientras que el opuesto es igual a xsen(θ).
También es importante considerar la orientación de sus componentes. Si el componente apunta en la dirección negativa de uno de los ejes, obtiene un signo menos. Por ejemplo, si un componente apunta hacia la izquierda o hacia abajo en el plano, recibe un signo menos.
Por ejemplo, digamos que tenemos un vector de magnitud 3 y dirección 135 con respecto a la horizontal. Con esta información podemos determinar que la componente x es igual a 3cos(135) = -2.12 y la componente y es 3sin(135) = 2.12

Imagen titulada Suma o resta vectores Paso 11

2. Suma las componentes correspondientes de dos o más vectores. Cuando hayas encontrado las componentes de todos los vectores, simplemente suma las magnitudes para encontrar las componentes de tu vector resultante. Primero sume los tamaños de los componentes horizontales (paralelos al eje x). Luego agregue los tamaños de los componentes verticales (paralelos al eje y). Si un componente tiene un signo menos (-) delante, su tamaño se resta. Las respuestas que obtienes son los componentes de tu vector resultante.

Por ejemplo, tomamos el vector del paso anterior, <-2.12 y 2.12>, y agregarlo al vector <5.78 y -9>. En este caso, nuestro vector resultante es <-2.12+5.78 y 2.12-9>, o <3,66 y -6,88>.

Imagen titulada Suma o resta vectores Paso 12

3. Calcule la magnitud del vector resultante usando el teorema de Pitágoras. Con esta declaración, c=a+b, ¿Puedes encontrar la longitud de los lados de los triángulos rectángulos?. Dado que el triángulo formado por el vector resultante y sus componentes es un triángulo rectángulo, podemos usar este teorema para encontrar la longitud del vector y, por lo tanto, su magnitud. De C como la magnitud del vector resultante que está tratando de encontrar, digamos a en como el tamaño de la componente x y B como la magnitud de la componente y. resolver con algebra.

Para encontrar la magnitud del vector cuyas componentes determinamos en el paso anterior, <3,66 y -6,88>, usamos el teorema de Pitágoras. Resolver de la siguiente manera:

c=(3.66)+(-6.88)

c=13,40+47,33

c=√60.73 = 7.79

Imagen titulada Suma o resta vectores Paso 13

4. Calcular la dirección de la resultante con la tangente. Finalmente, determinamos la dirección del vector resultante. Usa la fórmula θ=bronceado(b/a), donde θ es el ángulo que forma la resultante con el eje x desde la horizontal, donde b es la magnitud de la componente y y a es la magnitud de la componente x.

Para determinar la dirección de nuestro vector de ejemplo, usamos θ=tan(b/a).

θ=bronceado(-6.88/3.66)

θ=bronceado(-1.88)

θ=-61.99

Imagen titulada Suma o resta vectores Paso 14

5. Mostrar el vector resultante por tamaño y dirección. Como se indicó anteriormente, los vectores se definen por su magnitud y dirección. Asegúrese de utilizar las unidades correctas para el tamaño del vector.

Por ejemplo, si el vector de ejemplo representa una fuerza (en Newtons), podemos escribir esto como "un poder de 7.79 no en -61.99 desde la horizontal".

Consejos

Los vectores no deben confundirse con los tamaños.
Puedes encontrar el tamaño de un vector en el espacio mediante la fórmula a=b+c+d para usar, donde a es la magnitud del vector y antes de Cristo y D los componentes en cada dirección.
Vectores representados como xI + yj + zk se puede sumar o restar simplemente sumando o restando los coeficientes de los tres vectores. La respuesta entonces también está en la forma i, j, k.
Los vectores de columna se pueden sumar y restar, sumando o restando los valores en cada fila.