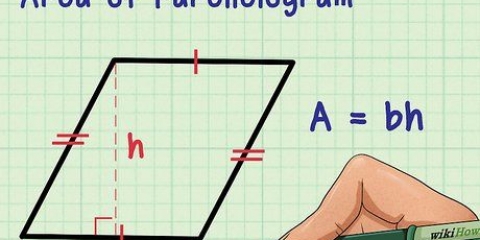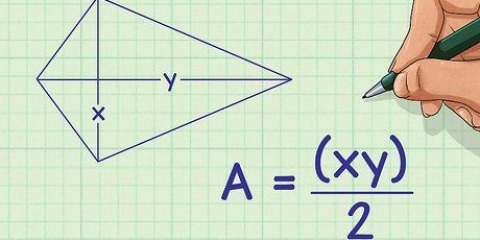Para formas pequeñas puedes usar centímetros, mientras que metros o kilómetros son más adecuados para circunferencias más grandes. Cuando los lados opuestos de los rectángulos son iguales, solo necesitas medir uno de los lados opuestos. 
Continúa con el ejemplo: imagina que además de un largo de 3 cm, el ancho de tu rectángulo es de 5 cm. 

Entonces, en este ejemplo, calculas 3 + 3 + 5 + 5 = 16 (el perímetro). También puede usar la fórmula 2 x (largo + ancho) para rectángulos, ya que el largo y el ancho de los lados opuestos son iguales y, por lo tanto, se duplican. Así que en nuestro ejemplo esto es: 2 x 8 = 16. 
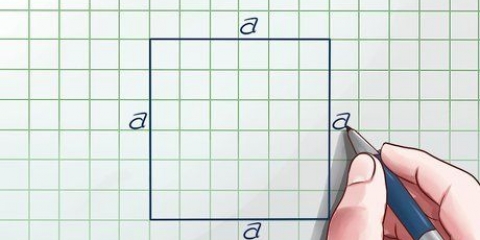
Cuadrado: largo de cada lado x 4 Triángulo: suma todos los lados Polígono irregular: suma todos los lados Círculo: 2 x π x radio o π x diámetro. El símbolo π significa Pi (pronunciado pastel). Si tiene una tecla π en su calculadora, puede usarla para ser más preciso al usar esta fórmula. Si no, puedes redondear el valor de π a 3.14. El término `radio` se refiere a la distancia entre el centro de un círculo y su límite exterior (circunferencia), mientras que `diámetro` se refiere a la longitud de una línea imaginaria entre dos puntos opuestos en la circunferencia de un círculo que pasa por el centro de el círculo, el círculo va. 

Puede dividir la forma en segmentos verticales y horizontales de una unidad (cm, m) si desea visualizar cómo se verá la medida del área. 
Puede escribir `unidades cuadradas/unidades cuadradas` como: cm² m² km² 
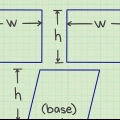
Paralelogramo: base x altura Cuadrado: lado 1 x lado 2 Triángulo: ½ x base x altura. Algunos matemáticos usan la notación: A=½bh. Círculo: π x r² (donde r = radio) El término "radio" se refiere a la distancia entre el centro de un círculo y su límite exterior (circunferencia), y el dos pequeño en superíndice (el cuadrado) indica que el valor al que pertenecen los dos se multiplica por sí mismo.
Determinar el área y el perímetro
Contenido
El perímetro es la longitud de todo el límite exterior de una figura plana (bidimensional), y el área es la medida de su tamaño. El área y el perímetro son medidas extremadamente útiles que se pueden usar en proyectos domésticos, de construcción, proyectos de bricolaje y al estimar la cantidad de materiales que puede necesitar. Por ejemplo, si desea pintar una habitación, necesitará saber cuánta pintura necesita o, en otras palabras, cuánto superficie la pintura puede cubrir. Lo mismo se puede decir al arreglar un jardín, construir una cerca o hacer otras tareas domésticas. En estas situaciones, puede usar el área y el perímetro para ahorrar tiempo y dinero al comprar materiales.
Pasos
Parte 1 de 2: Determinar la circunferencia

1. Determine la forma que desea medir. El perímetro es el límite exterior alrededor de una figura geométrica cerrada, y diferentes formas requerirán diferentes enfoques. Si la forma cuyo perímetro desea encontrar no es una forma cerrada, el perímetro no se puede determinar.
- Si es la primera vez que calcula el perímetro, pruebe con un rectángulo o un cuadrado. Estas formas regulares facilitan la determinación del perímetro.

2. Dibuja un rectángulo en una hoja de papel. Usas este rectángulo como forma de práctica y determinas su perímetro. Asegúrate de que los lados opuestos de tu rectángulo tengan la misma longitud.

3. Determinar la longitud de un lado de su rectángulo. Puedes hacer esto con una regla, una cinta métrica o inventando tu propio ejemplo. Escribe este número al lado del lado que representa, para que no olvides la longitud. Suponga que la longitud de un lado de su rectángulo es de 3 cm.

4. Determinar el ancho de un lado de su rectángulo. Puedes medir el ancho con una regla, cinta métrica o haciendo tu propio ejemplo. Escribe el valor de tu ancho al lado del lado horizontal de tu rectángulo que representa.

5. Escribe las medidas correctas en los lados opuestos de tu rectángulo. Los rectángulos tienen cuatro lados, pero la longitud de los lados opuestos será la misma. Esto también se aplica al ancho de su rectángulo. Escribe el largo y el ancho usados en el ejemplo (3 y 5 cm respectivamente) en los lados opuestos de tu rectángulo.

6. Suma todos los lados juntos. Debajo del ejemplo que hiciste o escribiste, escribe lo siguiente: largo + largo + ancho + ancho.

7. Ajuste su enfoque para diferentes formas. Desafortunadamente, diferentes formas requerirán diferentes fórmulas para el perímetro. En ejemplos del mundo real, puede medir el límite exterior de cualquier forma geométrica cerrada para determinar su perímetro. Pero también puedes usar las siguientes fórmulas para encontrar el perímetro de otras formas comunes:
Parte 2 de 2: Determinación del área

1. Determinar las dimensiones de su forma. Dibuja un rectángulo o usa el mismo rectángulo que dibujaste al determinar el perímetro. En este ejemplo, estás calculando el área de un rectángulo, usando su alto y ancho.
- Puedes trabajar con una regla o cinta métrica, o dar tu propio ejemplo. En este ejemplo, la longitud y el ancho son iguales al ejemplo anterior utilizado para encontrar el perímetro: 3 y 5. respectivamente.

2. Comprender el verdadero significado de la superficie. Determinar el área dentro de un perímetro es como dividir ese espacio vacío dentro de tu forma en 1 por 1. cuadrados. El área puede ser más pequeña o más grande que el perímetro, dependiendo de la forma.

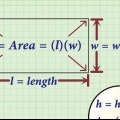
3. Multiplica el largo de tu rectángulo por el ancho. En el ejemplo: área = 3 x 5, que son 15 metros cuadrados. La unidad de medida del área siempre debe escribirse en unidades cuadradas (km cuadrados, metros cuadrados, etc.).).

4. Cambia tu fórmula dependiendo de la forma. Desafortunadamente, diferentes formas geométricas requerirán un enfoque diferente para calcular el área. Puedes usar las siguientes fórmulas para encontrar el área de algunas formas comunes:
Consejos
- Estas fórmulas de área y perímetro solo funcionan para el área (el volumen) de una forma plana. Si necesita encontrar el contenido de una forma tridimensional (el volumen), debe buscar fórmulas para el volumen, como las de conos, cubos, cilindros, prismas y pirámides.
Artículos de primera necesidad
- Papel
- Lápiz
- Calculadora (opcional)
- cinta métrica (opcional)
- regla (opcional)
Artículos sobre el tema. "Determinar el área y el perímetro"
Оцените, пожалуйста статью
Popular