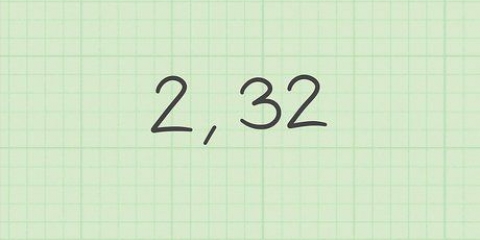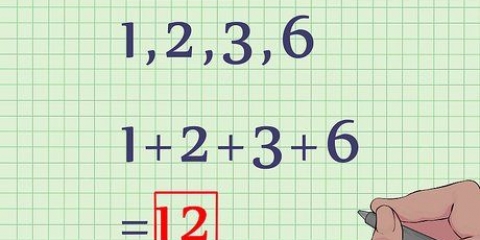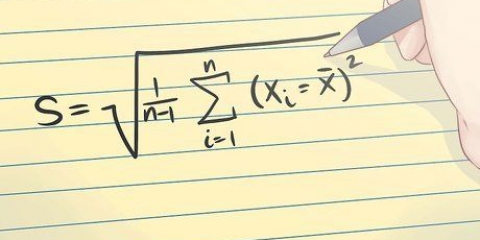En el ejemplo de recopilación de datos, estas variaciones se convierten en: 







Para verificar la validez de sus cálculos, verificamos si la suma de los valores en la columna de desviaciones es igual a cero. Si suma todas las desviaciones y obtiene algo distinto de cero, entonces su promedio es incorrecto o ha cometido un error en el cálculo de una o más de las desviaciones. Regresa y revisa tu trabajo. 
El valor absoluto es una herramienta matemática para indicar la distancia o la magnitud, independientemente de la dirección. Para determinar el valor absoluto, simplemente omita el signo menos para cada número en la segunda columna. Entonces llene la tercera columna con los valores absolutos de la siguiente manera: 









Para este conjunto de datos, el cálculo final será: 

Por ejemplo, con este conjunto de datos, puede decir que la media es nueve y la distancia media desde la media es 2,75. Tenga en cuenta que algunos valores están más cerca de 2.75 en comparación con otros. Pero 2.75 es la distancia promedio.
Cálculo de la desviación media de la media
Contenido
Cuando se trabaja con datos, hay varias formas de medir qué tan estrechamente se agrupan los valores de sus datos. El más común es el promedio. La mayoría de las personas aprenden a calcular la media temprano en la escuela al encontrar la suma de un grupo de valores de datos y luego dividir por la cantidad de valores en el grupo. Un cálculo más avanzado es la desviación media sobre la media. Este cálculo te dice qué tan cerca están tus valores de la media. Esto se determina encontrando la media de un conjunto de datos, luego la desviación de cada dato de esa media y luego la media de esas desviaciones.
Pasos
Parte 1 de 2: calcular el promedio

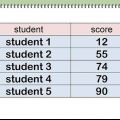
1. Recopile y cuente sus datos. Para cualquier conjunto de valores, la media es una medida del valor central. Según el tipo de datos, el promedio le dará el valor medio de esos datos. Para encontrar la media, primero debe recopilar sus datos, ya sea a través de un experimento o simplemente en una tarea.
- Como ejemplo usamos una secuencia numérica dada 6, 7, 10, 12, 13, 4, 8 y 12. Esta secuencia es lo suficientemente pequeña como para contarla a mano y ver rápidamente que es una secuencia de ocho números.
- Dentro del estadístico, la variable
o
a menudo se usa para indicar el número de valores en una serie o colección.

2. Encuentra la suma de los valores. El primer paso para determinar la media es calcular la suma de todos los valores. Dentro de la notación estadística, cada valor es generalmente representado por la variable  . A la suma de todos los valores se le da el símbolo
. A la suma de todos los valores se le da el símbolo  . La letra griega mayúscula sigma indica que es la suma de los valores. El cálculo para esta serie simple es así:
. La letra griega mayúscula sigma indica que es la suma de los valores. El cálculo para esta serie simple es así:
 . A la suma de todos los valores se le da el símbolo
. A la suma de todos los valores se le da el símbolo  . La letra griega mayúscula sigma indica que es la suma de los valores. El cálculo para esta serie simple es así:
. La letra griega mayúscula sigma indica que es la suma de los valores. El cálculo para esta serie simple es así:

3. Comparte para encontrar el promedio. Finalmente, divida la suma por el número de valores. La letra griega mu,  , se utiliza a menudo para indicar la media. Por lo tanto, el cálculo del promedio procede de la siguiente manera:
, se utiliza a menudo para indicar la media. Por lo tanto, el cálculo del promedio procede de la siguiente manera:
 , se utiliza a menudo para indicar la media. Por lo tanto, el cálculo del promedio procede de la siguiente manera:
, se utiliza a menudo para indicar la media. Por lo tanto, el cálculo del promedio procede de la siguiente manera:
Parte 2 de 2: encontrar la desviación promedio

1. crear una tabla. Para mantener sus datos en orden y ayudar con los cálculos, es útil crear una tabla de tres columnas. Etiqueta la primera columna  . Etiqueta la segunda columna
. Etiqueta la segunda columna  . Etiqueta la tercera columna
. Etiqueta la tercera columna  .
.
 . Etiqueta la segunda columna
. Etiqueta la segunda columna  . Etiqueta la tercera columna
. Etiqueta la tercera columna  .
. - Rellene la primera columna con los valores para su cálculo.

2. Calcular la desviación (desviación) de cada valor. En la segunda columna, etiquetada  , poner la desviación o diferencia entre cada valor y la media de la serie o conjunto. Encuentre este valor restando la media de cada valor de datos.
, poner la desviación o diferencia entre cada valor y la media de la serie o conjunto. Encuentre este valor restando la media de cada valor de datos.
 , poner la desviación o diferencia entre cada valor y la media de la serie o conjunto. Encuentre este valor restando la media de cada valor de datos.
, poner la desviación o diferencia entre cada valor y la media de la serie o conjunto. Encuentre este valor restando la media de cada valor de datos.








3. Determinar el valor absoluto de cada desviación. Cuando calcula la desviación de cada valor de la media, solo quiere saber la diferencia, no si esa diferencia es positiva o negativa. Lo que realmente necesitas, en términos matemáticos, es el valor absoluto de la diferencia. El valor absoluto se indica mediante barras verticales| |.










4. Calcular la media de las desviaciones absolutas. Después de completar la tabla de tres columnas, encuentre el promedio de los valores absolutos en la tercera columna. Tal como lo hizo para calcular el promedio de los valores iniciales, sume las desviaciones y divida la suma por el número de valores.


5. Interpretar el resultado. El valor de la desviación media de la media es una medida de qué tan cerca están los valores entre sí. Esto responde a la pregunta: "¿Qué tan cerca de la media están los valores de los datos en promedio?"?`
Consejos
- Sigue practicando y podrás calcularlo sin problemas.
Artículos sobre el tema. "Cálculo de la desviación media de la media"
Оцените, пожалуйста статью
Popular