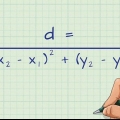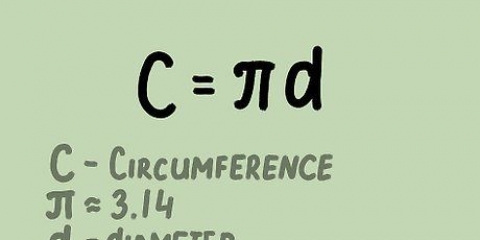Calcular la longitud del arco: 10 pasos (con fotos)

Contenido

Pasos
- Método 1 de 2: usar el ángulo central en grados
- Método 2 de 2: usar el ángulo central en radianes
Consejos

Un arco es cualquier parte de la circunferencia de un círculo. La longitud del arco es la distancia desde un extremo del arco hasta el otro. Calcular la longitud del arco requiere cierto conocimiento de la geometría de un círculo. Como el arco es parte del perímetro, puedes saber fácilmente cuál es la longitud del arco si sabes qué parte de los 360 grados es el ángulo central del arco.

Pasos

Método 1 de 2: usar el ángulo central en grados

Imagen titulada Encuentra la longitud del arco Paso 1

1. Escribe la fórmula para la longitud del arco. la fórmula es

longitud de arco = 2 π (r) (\frac{θ}{360})

${text{longitud de arco}}=2pi (r)({frac{theta }{360}})$ , por lo cual

r

$r$ es igual al radio del círculo y

θ

$theta$ es igual a la magnitud del ángulo del arco central, en grados.

2. Sustituye la longitud del radio del círculo en la fórmula. Esta información debe ser dada, o usted debe ser capaz de medirla. Asegúrese de ingresar la longitud del radio para la variable

r

$r$ .

Por ejemplo, si el radio del círculo es de 10 cm, la fórmula se vería así:

longitud de arco = 2 π (10) (\frac{θ}{360})

${text{longitud de arco}}=2pi (10)({frac{theta }{360}})$ .

3. Sustituye el valor del ángulo del arco central en la fórmula. Esta información debe ser dada, o usted debe ser capaz de medirla. Asegúrese de trabajar con grados (no radianes) al aplicar esta fórmula. Sustituye el ángulo del arco central por

θ

$theta$ en la fórmula.

Por ejemplo, si el ángulo del arco central es de 135 grados, la fórmula se vería así:

longitud de arco = 2 π (10) (\frac{135}{360})

${text{longitud de arco}}=2pi (10)({frac{135}{360}})$ .

Imagen titulada Encuentra la longitud del arco Paso 4

4. Multiplica el radio por 2π{ estilo de visualización 2 pi} $2pi$ . Si no usa calculadora, puede usar la aproximación

π = 3, 14

$pi = 3.14$ usar para los calculos. Reescribe la fórmula usando este nuevo valor (circunferencia del círculo).

Por ejemplo:

2 π (10) (\frac{135}{360})

$2pi (10)({frac{135}{360}})$

2 (3, 14) (10) (\frac{135}{360})

$2(3,14)(10)({frac{135}{360}})$

(62, 8) (\frac{135}{360})

$(62,8)({frac{135}{360}})$

Imagen titulada Encuentra la longitud del arco Paso 5

5. Divide el ángulo del arco central por 360. Dado que un círculo tiene un total de 360 grados, completar este cálculo te dará la parte del círculo completo que es igual a este segmento. Con esta información puedes encontrar la parte de la circunferencia que representa la longitud del arco.

Por ejemplo:

(62, 8) (\frac{135}{360})

$(62,8)({frac{135}{360}})$

(62, 8) (0, 375)

$(62.8)(0.375)$

Imagen titulada Encuentra la longitud del arco Paso 6

6. Multiplicar los dos números juntos. El resultado es la longitud del arco.

Por ejemplo:

(62, 8) (0, 375)

$(62.8)(0.375)$

23, 55

$23.55$
Entonces, la longitud del arco de un círculo con un radio de 10 cm y un ángulo central de 135 grados, es de aproximadamente 23,55 cm.

Método 2 de 2: usar el ángulo central en radianes

Imagen titulada Encuentra la longitud del arco Paso 7

1. Escribe la fórmula para la longitud del arco. la fórmula es

longitud de arco = θ (r)

${text{longitud de arco}}=theta (r)$ , donde

θ

$theta$ y es igual al valor del ángulo del arco central en radianes, y

r

$r$ es igual a la longitud del radio del circulo.

Imagen titulada Encuentra la longitud del arco Paso 8

2. Sustituye la longitud del radio del círculo en la fórmula. Necesitas la longitud del radio para este método. Asegúrese de usar la longitud del radio como el valor de la variable

r

$r$ .

Por ejemplo, si el radio del círculo es de 10 cm, la fórmula se vería así:

longitud de arco = θ (10)

${text{longitud de arco}}=theta (10)$ .

Imagen titulada Encuentra la longitud del arco Paso 9

3. Sustituye el valor del ángulo del arco central en la fórmula. Esta información debe ser dada en radianes. Si el valor del ángulo se da en grados, no puede usar este método.

Por ejemplo, si el ángulo del arco central es de 2,36 radianes, la fórmula se vería así:

longitud de arco = 2, 36 (10)

${text{longitud de arco}}=2.36(10)$ .

Imagen titulada Encuentra la longitud del arco Paso 10

4. Multiplica el radio por el valor del radián. El producto es la longitud del arco.

Por ejemplo:

2, 36 (10)

$2.36(10)$

= 23, 6

$=23,6$
Entonces, la longitud del arco de un círculo con un radio de 10 cm y un ángulo central de 2,36 radianes, es de aproximadamente 23,6 cm.

Consejos

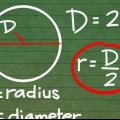
Si conoce el diámetro del círculo, también puede calcular la longitud del arco. Las fórmulas para encontrar la longitud del arco usan el radio del círculo. Como el radio es la mitad de un círculo, puedes encontrar el radio dividiendo el diámetro por 2. Por ejemplo, si el diámetro de un círculo es de 14 cm, entonces divide 14 entre 2 para encontrar el radio:
$14 \div 2 = 7$ $14 div 2 = 7$ .
entonces el radio del circulo es de 7 cm.