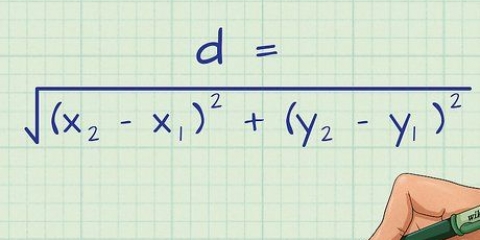Por ejemplo: mides la longitud de un campo de fútbol. Sabes que la longitud real o estándar de un campo de fútbol es de 100 metros. Entonces usas 100 como el valor real: .
. 
Por ejemplo: si mide el campo de fútbol y encuentra que tiene 90 metros de largo, entonces 90 es el valor medido: .
. 
Por ejemplo: porque  , es el error absoluto de su medida 10 metros.
, es el error absoluto de su medida 10 metros. 

Por ejemplo, si sabe que el error relativo es 0.025, su fórmula se vería así:  .
. 
Por ejemplo, si sabe que el valor real es 100 metros, su fórmula se vería así:  .
. 
Por ejemplo:




Por ejemplo:




Por ejemplo, si el valor medido es 104 metros y el valor real es 100 metros, entonces calcula  . Entonces el error absoluto es de 4 metros.
. Entonces el error absoluto es de 4 metros. 

Por ejemplo, si la unidad de medida es un metro, el margen de error máximo es de 0,5 metros. Entonces, la medida de un edificio se puede establecer como  metro. Esto significa que el valor real de la altura del edificio puede ser 0,5 metros más o menos que el valor medido. Si es más o menos, el valor medido sería 89 o 91 metros.
metro. Esto significa que el valor real de la altura del edificio puede ser 0,5 metros más o menos que el valor medido. Si es más o menos, el valor medido sería 89 o 91 metros. 
Por ejemplo: si mides que un edificio  metros, entonces el error absoluto es de 0,5 metros.
metros, entonces el error absoluto es de 0,5 metros.
Cálculo del error absoluto
Contenido
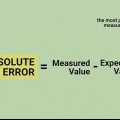
El error absoluto es la diferencia entre el valor medido y el valor real. Es una forma de considerar márgenes de error al medir la precisión de los valores. Si conoce los valores reales y medidos, calcular el error absoluto es una simple resta. Sin embargo, a veces no sabes cuál es el valor real, en cuyo caso debes considerar el error máximo posible como el error absoluto. Si conoce el valor real y el error relativo, puede trabajar hacia atrás para calcular el error absoluto.
Pasos
Método 1 de 3: Usar el valor real y el valor medido

1. Escriba la fórmula para calcular el error absoluto. la fórmula es  , por lo cual
, por lo cual  es igual al error absoluto (la diferencia entre, o el cambio de, el valor medido y el real),
es igual al error absoluto (la diferencia entre, o el cambio de, el valor medido y el real),  es igual al valor medido, y
es igual al valor medido, y  es igual al valor real.
es igual al valor real.
 , por lo cual
, por lo cual  es igual al error absoluto (la diferencia entre, o el cambio de, el valor medido y el real),
es igual al error absoluto (la diferencia entre, o el cambio de, el valor medido y el real),  es igual al valor medido, y
es igual al valor medido, y  es igual al valor real.
es igual al valor real.
2. Introduzca el valor real en la fórmula. El valor real debe ser dado. De lo contrario, utilice un valor predeterminado aceptable. Sustituya este valor por  .
.
 .
. .
.
3. Determinar el valor medido. Esto se da, o tienes que realizar la medición tú mismo. Sustituya este valor por  .
.
 .
. .
.
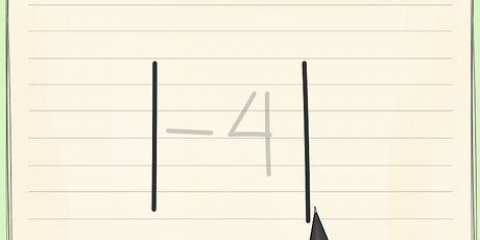
4. Reste el valor real del valor medido. Dado que el error absoluto siempre es positivo, tome el valor absoluto de esta diferencia, ignorando cualquier signo menos. Esto te da el error absoluto.
 , es el error absoluto de su medida 10 metros.
, es el error absoluto de su medida 10 metros.Método 2 de 3: usar el valor real y el error relativo

1. Escriba la fórmula para el error relativo. la fórmula es  , por lo cual
, por lo cual  es igual al error relativo (la relación entre el error absoluto y el valor real),
es igual al error relativo (la relación entre el error absoluto y el valor real),  es igual al valor medido, y
es igual al valor medido, y  es igual al valor real.
es igual al valor real.
 , por lo cual
, por lo cual  es igual al error relativo (la relación entre el error absoluto y el valor real),
es igual al error relativo (la relación entre el error absoluto y el valor real),  es igual al valor medido, y
es igual al valor medido, y  es igual al valor real.
es igual al valor real.
2. Introduzca el valor del error relativo. Esto es probablemente un decimal. Asegúrese de sustituir esto por  .
.
 .
. .
.
3. Introduzca el valor para el valor real. esto se debe dar. Sustituya este valor por  .
.
 .
. .
.
4. Multiplica cada lado de la ecuación por el valor real. Esto elimina la fracción.




5. Agregue el valor real a cada lado de la ecuación. Esto le dará el valor de  y por lo tanto el valor medido.
y por lo tanto el valor medido.
 y por lo tanto el valor medido.
y por lo tanto el valor medido.



6. Reste el valor real del valor medido. Dado que el error absoluto siempre es positivo, tome el valor absoluto de esta diferencia e ignore los signos menos. Esto te da el error absoluto.
 . Entonces el error absoluto es de 4 metros.
. Entonces el error absoluto es de 4 metros.Método 3 de 3: usar el margen de error máximo

1. Determina qué unidad de medida usas. Este es el valor `preciso a la [unidad]`. Esto se puede establecer explícitamente (p.: `El edificio se midió con precisión al centímetro`), pero ese no tiene por qué ser el caso. Determine la unidad de medida observando el número de lugares decimales a los que se redondea la medida.
- Por ejemplo, si la longitud medida de un edificio es de 100 metros, sabrá que el edificio se ha medido al metro más cercano. Entonces la unidad de medida es el metro.

2. Determinar el margen máximo de error. El margen máximo de error es  la unidad de medida. Esto puede aparecer como
la unidad de medida. Esto puede aparecer como  un número.
un número.
 la unidad de medida. Esto puede aparecer como
la unidad de medida. Esto puede aparecer como  un número.
un número. metro. Esto significa que el valor real de la altura del edificio puede ser 0,5 metros más o menos que el valor medido. Si es más o menos, el valor medido sería 89 o 91 metros.
metro. Esto significa que el valor real de la altura del edificio puede ser 0,5 metros más o menos que el valor medido. Si es más o menos, el valor medido sería 89 o 91 metros.
3. Usar el margen máximo de error como el error absoluto. Dado que el error absoluto siempre es positivo, tomamos el valor absoluto de esta diferencia, ignorando cualquier signo menos. Esto te da el error absoluto.
 metros, entonces el error absoluto es de 0,5 metros.
metros, entonces el error absoluto es de 0,5 metros.Consejos
- Si no se proporciona el valor real, puede buscar el valor estándar o teórico.
Artículos sobre el tema. "Cálculo del error absoluto"
Оцените, пожалуйста статью
Similar
Popular