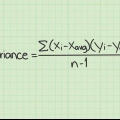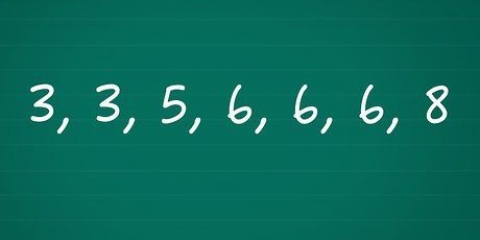Cómo calcular el coeficiente de correlación de rango de Spearman

Contenido

Pasos
Consejos
Advertencias

Con el coeficiente de correlación de rangos de Spearman, puede ver si dos variables están relacionadas por una función monótona (d.w.z. que si un número aumenta, el otro número también aumenta o viceversa). Para calcular el coeficiente de correlación de rangos de Spearman, debe ordenar y comparar conjuntos de datos para encontrar Σd, luego ingrese ese valor en la versión estándar o simplificada de la fórmula del coeficiente de correlación de rangos de Spearman. También puede calcular este coeficiente con fórmulas de Excel o comandos R.

Pasos

Método 1 de 3: manualmente

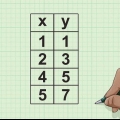
1. Dibuja tu tabla de datos. Organiza la información que necesita para calcular el coeficiente de correlación de rango de Spearman. Necesitas:

6 columnas de encabezados, como se muestra arriba.
Tantas filas como pares de datos tengas.

2. Complete las dos primeras columnas con sus pares de datos.

3. Organice los puntos de datos de la primera columna en la tercera columna, del 1 al norte (el número total de puntos de datos que tiene). Dar el número más bajo en la posición 1, el siguiente número en la posición 2, y así sucesivamente.

4. Haga lo mismo con la cuarta columna que en el paso 3, pero ahora organice la segunda columna.

Si tiene dos (o más) puntos de datos con el mismo valor en una columna, tome el promedio de las posiciones que normalmente tendrían esos puntos de datos y proporcione a los puntos de datos este promedio como su nueva posición.
En el ejemplo de la derecha hay dos cincos que normalmente estarían en la posición 2 y 3. Son dos las mismas canciones, así que tomar el promedio de sus puestos. La media de 2 y 3 es 2,5, así que da a ambos cincos la posición 2,5.

5. En la columna `d`, calcule la diferencia entre las dos posiciones en cada par de datos. En otras palabras, si uno tiene la posición 1 y el otro tiene la posición 3, la diferencia es 2. (Positivo o negativo no importa, ya que vamos a elevar al cuadrado esta diferencia en el siguiente paso.)

6. Cuadre los valores en la columna d y escriba estos valores en la columna d.

7. Agregue todos los puntos de datos en la columna d juntos. Este valor es Σd.

8. Elija una de las siguientes fórmulas:

Si no ocurrieron puntos de datos iguales en los pasos anteriores, ingrese Σd en la fórmula simple para el coeficiente de correlación de rango de Spearman

e ingrese el número de pares de datos para `n` para encontrar su respuesta.

Si ocurrieron puntos de datos similares en los pasos anteriores, use la fórmula estándar para el coeficiente de correlación de rango de Spearman:

9. Interpretar el resultado. Esto puede variar entre -1 y 1.

Cerca de -1 – Correlación negativa.

Cerca de 0: sin correlación lineal.

Cercano a 1 – Correlación Positiva.

Método 2 de 3: en Excel

1. Crear nuevas columnas con las posiciones de las columnas existentes. Por ejemplo, si tiene sus datos en la columna A2:A11, usaría la fórmula `=RANK(A2,A$2:A$11)` y extendería el rango a todas sus filas y columnas.

2. Trate puntos de datos iguales como se describe en los pasos 3 y 4 del método 1.

3. En una nueva celda, haga un cálculo de correlación entre las dos columnas con una fórmula como `=CORREL(C2:C11,D2:D11)`. En este caso, C y D son las columnas de posición. El coeficiente de correlación de rango de Spearman aparece en la celda de correlación.

Método 3 de 3: Con R

1. Instala R si aún no lo tienes. (Ver https://www.proyecto r.org/.)

2. Guarde sus datos como un archivo CSV, con los datos que desea correlacionar en las dos primeras columnas. Puede hacerlo con el menú `Guardar como`.

3. Abre el editor de R. Si está trabajando en la terminal, simplemente ejecute R. Cuando esté en su escritorio, haga clic en el logotipo R.

4. Escriba los siguientes comandos:

D <- leer.CSV("NOMBRE_DE_TU_CSV.CSV") y presiona enter

cor(rango(d[,1]),rango(d[,2]))

Consejos

Para la mayoría de los conjuntos de datos, necesita al menos cinco pares de datos para establecer una tendencia (solo se usaron tres pares en el ejemplo para facilitar el ejemplo).

Advertencias

El coeficiente de correlación de rango de Spearman solo muestra la fuerza de la correlación si los puntos de datos aumentan o disminuyen continuamente. Si el diagrama de dispersión de los puntos de datos muestra una tendencia diferente, el coeficiente de correlación de rangos de Spearman aumentará la correlación no mostrar correctamente.
Esta fórmula se basa en la suposición de que no hay puntos de datos iguales. Si hay puntos de datos iguales, como en el ejemplo anterior, use la siguiente definición: el coeficiente de correlación producto-momento para los rangos.