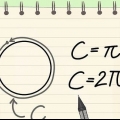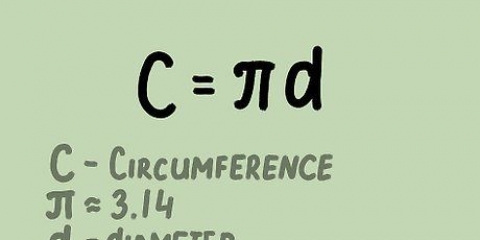Memorizar el círculo unitario: 14 pasos (con fotos)

Contenido

Pasos
- Parte 1 de 2: recuerda los radianes
- Parte 2 de 2: recuerda las coordenadas x e y (coseno, seno)
Consejos

Aprender el círculo unitario te ayudará no solo con la trigonometría y la geometría, sino también con el cálculo diferencial e integral. Puede parecer mucha memorización, pero una vez que comprenda cómo funciona, puede comenzar con algunos números del círculo unitario y descubrir rápidamente el resto.

Pasos

Parte 1 de 2: recuerda los radianes

Imagen titulada Memoriza el círculo unitario Paso 1

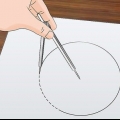
1. Dibujar dos rectas perpendiculares. Coloque una brújula en una hoja grande de papel. Dibuja una línea vertical y una horizontal. Estos deben cruzarse cerca del centro de la página. Estos son el eje x y el eje y del gráfico.

Imagen titulada Memoriza el círculo unitario Paso 2

2. Dibuja un circulo. Usando un compás, dibuja un círculo grande centrado en la intersección de las dos líneas.

Imagen titulada Memoriza el círculo unitario Paso 3

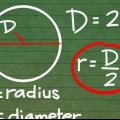
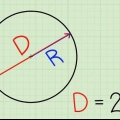
3. entender radianes. Un radián es una medida de ángulo. Se define principalmente de tal manera que una persona que camina alrededor de un círculo con un Rayo de 1 unidad se mueve a través de un ángulo de un radián después de caminar 1 unidad alrededor del perímetro. En el siguiente paso, indicaremos los cuatro puntos de coordenadas con el valor en radianes. Si recuerdas la fórmula de la relación entre la circunferencia de un círculo y su radio, puedes resolverla rápidamente, pero incluso si no la recuerdas.

Las medidas en radianes del círculo unitario siempre asumen que comienzas desde el punto (0, 1). Para que quede claro a qué punto nos referimos, describimos el círculo como una rosa de los vientos:

Imagen titulada Memoriza el círculo unitario Paso 4

4. Recuerda que la circunferencia del círculo es 2π. La circunferencia de un círculo es igual a 2πr, por lo cual r representa el radio (el radio). Como el círculo unitario tiene un radio de 1, podemos simplificar la circunferencia a 2π. El valor en radianes de cualquier punto de la circunferencia se puede encontrar simplemente dividiendo 2π por la parte del círculo que tenía. Esto es mucho más fácil que memorizar cada valor individual en el círculo.

Imagen titulada Memoriza el círculo unitario Paso 5

5. Indique los cuatro puntos en los ejes x e y. Todo lo que necesitas hacer es dividir 2π en cuartos:

`Este` es el punto de partida, por lo que tiene 0 tenía radianes.

`Norte` = un cuarto de la circunferencia del círculo = /₄ = /₂ radianes.

`Oeste` = a la mitad del círculo = /₂ = π radianes.

`Sur` = tres cuartos del círculo = 2π * ¾ = /₂ radianes.

Si recorres todo el perímetro, vuelves al punto de partida. Puedes indicar esto como 2π o 0.

Imagen titulada Memoriza el círculo unitario Paso 6

6. Divide el círculo en ocho piezas. Ahora dibuja una línea diagonal a través de cada cuadrante, perfectamente a través del centro. De nuevo, usa la división para encontrar el valor en radianes:

/₄

(π/2, π, 3π/2 y 2π ya han sido indicados.)

Imagen titulada Memoriza el círculo unitario Paso 7

7. Divide el círculo en seis segmentos. Ahora dibuja líneas adicionales que dividan el círculo en seis segmentos. (Puedes usar un transportador para esto, comenzando en el eje x positivo, donde cada segmento mide 60 grados). Puede usar el mismo enfoque que el anterior para asegurarse de que un sexto de un círculo sea igual a /₆ = /₃ radianes. Utilice esta etiqueta para los siguientes puntos del perímetro (uno en cada cuadrante):

/₃

(π y 2π ya están indicados)

Imagen titulada Memoriza el círculo unitario Paso 8

8. Dibuja los doceavos en él. Los últimos puntos marcados en la mayoría de los círculos unitarios indican incrementos de una doceava parte de la circunferencia. Solo cuatro de ellos aún no han sido declarados:

/₆

Parte 2 de 2: recuerda las coordenadas x e y (coseno, seno)

Imagen titulada Memoriza el círculo unitario Paso 9

1. Comprender coseno y seno. El círculo unitario es especialmente útil para cálculos trigonométricos con ángulos rectos. Cada coordenada x de un punto en el círculo es igual a cos(θ) y cada coordenada y es igual a sin(θ), donde θ es el valor del ángulo.

Si le resulta difícil recordar, piense en (cos, sin) `porque el seno es el último`.
Puedes deducir esto usando triángulos rectángulos y la definición de estas funciones, recuerda `soscastoa`?

Imagen titulada Memoriza el círculo unitario Paso 10

2. Escribe las coordenadas en cuatro puntos del círculo. Un `círculo unitario` es simplemente un círculo con un radio de exactamente una unidad. Úselos para encontrar las coordenadas x e y de los cuatro puntos en el círculo donde se cruza con un eje. (Los llamamos `Este`, `Norte`, etc. para facilitar la lectura, pero estos no son nombres oficiales).

Las coordenadas de `Este` son (1, 0).

Las coordenadas de `Norte` son (0, 1).

Las coordenadas de `Oeste` son (-1, 0).

Las coordenadas de `Sur` son (0, -1).

Esto funciona como un gráfico normal. Debería poder encontrar estas coordenadas usted mismo, sin tener que memorizarlas.

Imagen titulada Memoriza el círculo unitario Paso 11

3. Memoriza las coordenadas del primer cuadrante. El primer cuadrante es el cuarto superior derecho del círculo, donde tanto el valores x como el y-los valores son positivos. Estas son las únicas coordenadas que necesita recordar:

Sobre /₆, son las coordenadas ( $\frac{\sqrt{3}}{2}, \frac{1}{2}$ ${frac{{sqrt{3}}}{2}},{frac{1}{2}}$ ).

Sobre /₄, son las coordenadas ( $\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}$ ${frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ).

Sobre /₃, son las coordenadas ( $\frac{1}{2}, \frac{\sqrt{3}}{2}$ ${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ).

Tenga en cuenta que solo hay tres contadores. ¿Se está moviendo en una dirección positiva (de izquierda a derecha para el valores x, de abajo hacia arriba para el valores de y), entonces la secuencia es la siguiente: 1 → √2 → √3.

Imagen titulada Memoriza el círculo unitario Paso 12

4. Dibuja líneas rectas para completar las otras coordenadas. Si puede dibujar una línea perfectamente vertical o perfectamente horizontal entre dos puntos, entonces tienen el mismo valor absoluto que las coordenadas x e y. En otras palabras, puede dibujar una línea desde un punto en los primeros cuadrantes, escribir las mismas coordenadas donde aterriza y dejar espacio a la derecha para el signo (+ o -).

Por ejemplo, puede dibujar una línea horizontal entre /₃ y /₃. Dado que las coordenadas en el primer punto (

\frac{1}{2}, \frac{\sqrt{3}}{2}

${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ), las coordenadas del segundo punto (?

\frac{1}{2}, ? \frac{\sqrt{3}}{2}

${frac{1}{2}},?{frac{{sqrt{3}}}{2}}$ ), por lo que `?` representa un signo más o menos (+ o -).

Aquí hay una forma más rápida: verifica el denominador de los radianes. Todos los puntos que terminan en /3 tienen las mismas coordenadas absolutas, al igual que todos los puntos que terminan en /4 y todos los puntos que terminan en /6.

Imagen titulada Memoriza el círculo unitario Paso 13

5. Usa la simetría para saber si el signo es positivo o negativo. Hay varias formas de recordar dónde colocar los signos menos en el círculo unitario:

Piense en las reglas fundamentales para los gráficos. Sobre el X-eje los puntos son positivos, debajo de él negativos. A la izquierda de la y es negativo, la derecha es positiva.

Comience desde el cuadrante 1 y dibuje líneas a otros puntos. Si la línea de y-el eje cruza el valor y cambiará de signo. Si la línea de X-el eje se cruza, entonces el valor de x cambia de signo.

Aprenda `Todos los estudiantes prueban cálculo` (ASTC), en sentido contrario a las agujas del reloj. El cuadrante 1 tiene asolo valores positivos, el cuadrante 2 solo tiene valores positivos sinus valores, el cuadrante 3 tiene sólo positivo tangens valores, y el cuadrante 4 tiene sólo positivo Cvalores de oseno.

Independientemente del método que elija, los signos son (+, +) para el cuadrante 1, (-, +) para el cuadrante 2, (-, -) para el cuadrante 3 y (+,-) para el cuadrante 4.

Imagen titulada Memoriza el círculo unitario Paso 14

6. Revisa tu trabajo. Aquí está la lista completa de valores de coordenadas para cada punto etiquetado en el círculo (sin contar los cuatro puntos en los ejes), en el sentido de las agujas del reloj. Recuerda, deberías poder encontrar todos estos valores simplemente memorizando los puntos del cuadrante 1:

Cuadrante 1: (

\frac{\sqrt{3}}{2}, \frac{1}{2}

${frac{{sqrt{3}}}{2}},{frac{1}{2}}$ ); (

\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}

${frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ); (

\frac{1}{2}, \frac{\sqrt{3}}{2}

${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ).

Cuadrante 2: (

- \frac{1}{2}, \frac{\sqrt{3}}{2}

$-{frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ); (

- \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}

$-{frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ); (

- \frac{\sqrt{3}}{2}, \frac{1}{2}

$-{frac{{sqrt{3}}}{2}},{frac{1}{2}}$ )

Cuadrante 3: (

- \frac{\sqrt{3}}{2}, - \frac{1}{2}

$-{frac{{sqrt{3}}}{2}},-{frac{1}{2}}$ ); (

- \frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2}

$-{frac{{sqrt{2}}}{2}},-{frac{{sqrt{2}}}{2}}$ ); (

- \frac{1}{2}, - \frac{\sqrt{3}}{2}

$-{frac{1}{2}},-{frac{{sqrt{3}}}{2}}$ )

Cuadrante 4: (

\frac{1}{2}, - \frac{\sqrt{3}}{2}

${frac{1}{2}},-{frac{{sqrt{3}}}{2}}$ ); (

\frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2}

${frac{{sqrt{2}}}{2}},-{frac{{sqrt{2}}}{2}}$ ); (

\frac{\sqrt{3}}{2}, - \frac{1}{2}

${frac{{sqrt{3}}}{2}},-{frac{1}{2}}$ )

Consejos

Si tiene una prueba o ensayo sobre el círculo unitario, primero dibuje el círculo en papel borrador para que pueda usarlo como referencia para cada problema.
El proceso será considerablemente más rápido si practicas mucho. En el futuro, es posible que solo necesite ver los ejes x e y para recordar todo, o es posible que ya no necesite un gráfico.