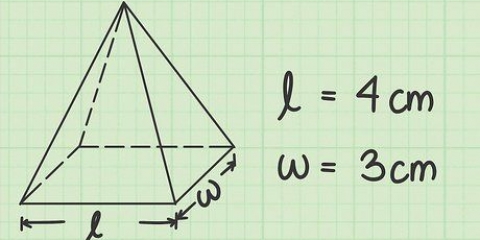Por ejemplo, si quieres encontrar el área de una pirámide hexagonal y sabes que la longitud de una arista de la base es de 4 cm, calculas  para encontrar el perímetro de la base, porque un hexágono tiene seis lados. Entonces, el perímetro de la base es de 24 cm, por lo que la fórmula para el área se verá así:
para encontrar el perímetro de la base, porque un hexágono tiene seis lados. Entonces, el perímetro de la base es de 24 cm, por lo que la fórmula para el área se verá así:  .
. 
Suponga que la altura inclinada de una pirámide hexagonal es de 12 cm, entonces su fórmula se verá así:  .
. 
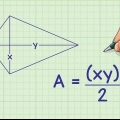
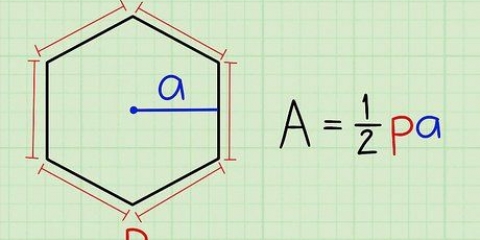
Por ejemplo, si se trata de una pirámide hexagonal, debe calcular el area del hexagono. la fórmula es  , por lo cual
, por lo cual  es la longitud de un lado del hexágono. Dado que la longitud de un lado del hexágono es de 4 cm, calcule de la siguiente manera:
es la longitud de un lado del hexágono. Dado que la longitud de un lado del hexágono es de 4 cm, calcule de la siguiente manera:




 .
.
entonces el area de la base es 41.57 centimetros cuadrados. 
Supongamos que el área de la base hexagonal es de 41,57 cm. entonces su fórmula para el área se vería así:  .
. 
Por ejemplo:




Por ejemplo:


Entonces, el área total de una pirámide hexagonal, con una longitud de arista base dada de 4 cm y una altura de pendiente de 12 cm, es igual a 185,57 centímetros cuadrados. 

Suponga que la longitud de un lado de la base de una pirámide cuadrada es de 4 cm y la altura de la pendiente es de 12 cm, entonces la fórmula se vería así:  .
. 
Por ejemplo:



Por ejemplo:





Por ejemplo:


El área total de una pirámide cuadrada, con un lado de la base de 4 cm y una altura oblicua de 12 cm, es por lo tanto 112 centímetros cuadrados.
Determinando el área de una pirámide
Contenido
El área de una pirámide se puede encontrar sumando el área de su base al área de sus lados. Cuando trabajes con pirámides regulares puedes encontrar el área usando una fórmula siempre y cuando sepas cómo encontrar el área de la base de la pirámide. Dado que la base puede ser un polígono, es útil saber cómo determinar el área de formas como pentágonos y hexágonos. Sin embargo, cuando se trabaja con la pirámide cuadrada regular regular, calcular el área total es fácil, siempre que conozca la altura inclinada de la pirámide y la longitud de la base cuadrada.
Pasos
Método 1 de 2: encontrar el área de una pirámide común

1. Escribe la formula del area de una piramide ordinaria. la fórmula es  , por lo cual
, por lo cual  es igual al area total de la piramide,
es igual al area total de la piramide,  es igual al perímetro de la base,
es igual al perímetro de la base,  es igual a la pendiente de la pirámide, y
es igual a la pendiente de la pirámide, y  es igual al area de la base.
es igual al area de la base.
 , por lo cual
, por lo cual  es igual al area total de la piramide,
es igual al area total de la piramide,  es igual al perímetro de la base,
es igual al perímetro de la base,  es igual a la pendiente de la pirámide, y
es igual a la pendiente de la pirámide, y  es igual al area de la base.
es igual al area de la base. - La fórmula básica para el área de una pirámide, regular o irregular, es Área Total = Área Base + Área Inclinada.
- No confunda `altura inclinada` con `altura.La `altura inclinada` es la distancia diagonal desde la parte superior de la pirámide hasta el borde de la base. La `altura` es la distancia perpendicular desde la parte superior a la base.

2. Calcular el perímetro de la base. Si no se da el perímetro, pero se da la longitud de un borde de la base, puede calcular el perímetro multiplicando la longitud de un borde por el número de bordes.
 para encontrar el perímetro de la base, porque un hexágono tiene seis lados. Entonces, el perímetro de la base es de 24 cm, por lo que la fórmula para el área se verá así:
para encontrar el perímetro de la base, porque un hexágono tiene seis lados. Entonces, el perímetro de la base es de 24 cm, por lo que la fórmula para el área se verá así:  .
.
3. Ingrese el valor de la altura de la pendiente en la fórmula. Asegúrese de utilizar la altura inclinada, no la altura perpendicular. La altura de la pendiente se debe dar en el problema. Si no conoce la altura de la pendiente, no puede usar este método.
 .
.
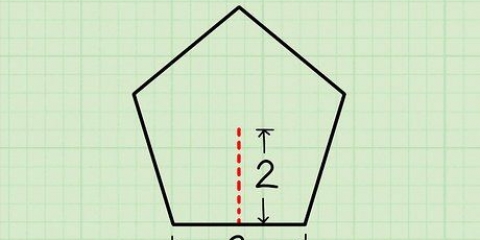
4. Calcular el área de la base. Cómo lo haces depende de la forma de la base. Para eso necesitas saber como determinar las areas de poligonos.
 , por lo cual
, por lo cual  es la longitud de un lado del hexágono. Dado que la longitud de un lado del hexágono es de 4 cm, calcule de la siguiente manera:
es la longitud de un lado del hexágono. Dado que la longitud de un lado del hexágono es de 4 cm, calcule de la siguiente manera: 



 .
.entonces el area de la base es 41.57 centimetros cuadrados.

5. Aplicar el área de la base a la fórmula. Asegúrate de tener la variable  reemplaza.
reemplaza.
 reemplaza.
reemplaza. .
.
6. Multiplica el perímetro de la base por la altura inclinada de la pirámide. Dividir el producto por dos. Esto te da el área inclinada de las caras de la pirámide.




7. Suma los dos valores juntos. La suma es el área inclinada más el área de la base, por lo que obtienes el área total de la pirámide en unidades cuadradas.


Entonces, el área total de una pirámide hexagonal, con una longitud de arista base dada de 4 cm y una altura de pendiente de 12 cm, es igual a 185,57 centímetros cuadrados.
Método 2 de 2: encontrar el área de una pirámide cuadrada

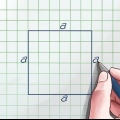
1. Escribe la formula del area de una piramide cuadrada. la fórmula es  , por lo cual
, por lo cual  es igual a la longitud de un lado de la base, y
es igual a la longitud de un lado de la base, y  es igual a la pendiente de la piramide.
es igual a la pendiente de la piramide.
 , por lo cual
, por lo cual  es igual a la longitud de un lado de la base, y
es igual a la longitud de un lado de la base, y  es igual a la pendiente de la piramide.
es igual a la pendiente de la piramide. - No confunda `altura inclinada` con `altura.La `altura inclinada` es la distancia diagonal desde la parte superior de la pirámide hasta el borde de la base. La `altura` es la distancia perpendicular desde la parte superior a la base.
- Tenga en cuenta que esta fórmula es solo otra forma de calcular el Área total = Área base (
) + Superficie inclinada (
) escribir. Esta fórmula solo funciona para pirámides cuadradas regulares.

2. Ingrese los valores de la longitud de los lados y la altura de la pendiente en la fórmula. Asegúrese de reemplazar la longitud del lado de la base con  y la altura inclinada por
y la altura inclinada por  .
.
 y la altura inclinada por
y la altura inclinada por  .
. .
.
3. Cuadrar la longitud de un lado de la base. Esto te dará el área de la base.



4. Multiplique la longitud de un lado de la base por la altura de la pendiente y divida por dos. Luego multiplica por cuatro. Esto le dará la superficie en ángulo de la pirámide.





5. Suma el área de la base a esa área inclinada. Esto te dará el área total de la pirámide, en unidades cuadradas.


El área total de una pirámide cuadrada, con un lado de la base de 4 cm y una altura oblicua de 12 cm, es por lo tanto 112 centímetros cuadrados.
Artículos de primera necesidad
- Lápiz
- Papel
- Calculadora (opcional)
- regla (opcional)
Artículos sobre el tema. "Determinando el área de una pirámide"
Оцените, пожалуйста статью
Popular