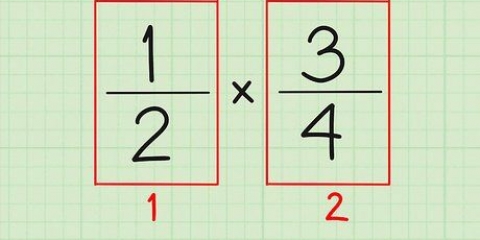
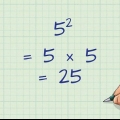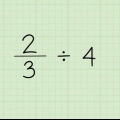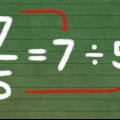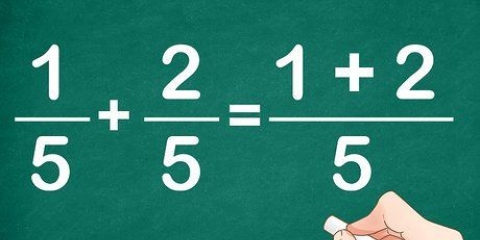el recíproco de 3/4 es 4/3. El recíproco de 7/5 es 5/7. El recíproco de 1/2 es 2/1 y por lo tanto 2. 
Dejar el contador sin cambios. Haz que el signo de división sea una multiplicación. Haz el inverso de la segunda fracción. Multiplica los numeradores de las dos fracciones. El resultado será el contador de tu respuesta. Multiplica los denominadores de las dos fracciones. El resultado será el denominador de tu respuesta. simplifica la fraccion. 
1/3 ÷ 2/5 = se está convirtiendo: 1/3 * __ = Ahora rotamos la segunda fracción (2/5). Esto entonces se convierte en 5/2: 1/3 * 5/2 = Ahora multiplicamos los numeradores de las dos fracciones, 1*5 = 5. 1/3 * 5/2 = 5/ Ahora multiplicamos los denominadores de las dos fracciones, 3*2 = 6. Ahora tenemos: 1/3 * 5/2 = 5/6 Esta fracción en particular no se puede simplificar más, así que ahora tenemos nuestra respuesta. 



2/3 * 7/3 = __ 

Comparte el contador primero 14 por medio de 9.9 cabe en 14 una vez, con un resto de 5, por lo que puedes escribir esto como: 1 5/9. Puedes parar ahora, porque has encontrado la respuesta! Puedes ver que esta fracción no se puede simplificar más, porque 9 no es completamente divisible por 5 y porque el numerador es un número primo. 
Primero divide el numerador por el denominador, (24/10 = 2 resto 4). Escribe la respuesta como 2 4/10. Pero podemos simplificar esta fracción aún más! Tenga en cuenta que 4 y 10 son números pares, por lo que el primer paso es simplificar dividiéndolos por 2.la fraccion ahora es 2/5. Como el denominador (5) no encaja completamente en el numerador (2) y también es primo, sabes que no puedes simplificar más esta fracción. Entonces la respuesta es: 2 2/5. 
Dividir fracciones por fracciones
Contenido
Dividir una fracción entre una fracción puede parecer confuso al principio, pero en realidad es muy simple. Todo lo que tienes que hacer es invertir la fracción inferior o segunda, luego multiplicar ambas fracciones juntas! Este artículo te mostrará cómo hacer esto y te mostrará que dividir fracciones por fracciones no debería ser un problema en absoluto.
Pasos
Parte 1 de 2: entender cómo funciona

1. Piensa en lo que significa dividir por una fracción.El ejercicio 2 ÷ 1/2 dice lo mismo que: ”¿Cuántas veces cabe ½ en 2?”La respuesta es 4, porque puedes dividir 2 en 4 mitades.
- También trata de pensar en este problema en términos de vasos de agua: ¿Cuántos medios vasos de agua hay en 2 vasos de agua?? Esto lo puedes solucionar echando 2 medios vasos de agua en otro vaso, de manera que al final tengas 2 vasos llenos de agua: 2 medios/1 vaso * 2 vasos = 4 medios vasos.
- Esto significa que si divides un número entre un número entre 0 y 1, la respuesta siempre será mayor que ese número! Esto es cierto ya sea que divida un número entero o una fracción por otra fracción.

2. La división es lo opuesto a la multiplicación.Entonces también puedes pensar en dividir por una fracción como multiplicar por el recíproco de esa fracción.El inverso de una fracción es lo que dice, simplemente intercambiando el numerador y el denominador. En un momento vamos a dividir fracciones por fracciones multiplicando por el recíproco del denominador, pero por ahora veremos algunos inversos de fracciones:

3. Recuerda los siguientes pasos para dividir una fracción entre otra fracción.Estos son los pasos en orden:

4. Realice estos pasos en el ejemplo 1/3 ÷ 2/5.Dejamos el numerador (la primera fracción) sin cambios y cambiamos el signo de división a un signo de tiempo:

5. Trate de recordar lo siguiente:"Dividir por una fracción es lo mismo que multiplicar por el recíproco."
Parte 2 de 2: Dividir fracciones por fracciones - ejemplos

1. Comience con un problema de ejemplo. Supongamos que tenemos la tarea 2/3 3/7. La pregunta aquí es con qué frecuencia 3/7 cabe en 2/3. No entrar en pánico; no es tan difícil como parece!

2. Haz que el signo de división sea un signo de multiplicación. La tarea ahora se convierte en: 2/3 * __ (llenaremos el campo vacío en un momento.)

3. Ahora determinamos el recíproco de la segunda fracción.Esto significa que volteamos 3/7 para que el numerador se convierta en 3 y el denominador se convierta en 7.El recíproco de 3/7 es 7/3.Ahora escribimos el nuevo problema:

4. Multiplica las fracciones.Primero, multiplicamos los numeradores de las dos fracciones: 2 * 7 = 14.14 es el numerador de tu respuesta.Luego multiplicamos los denominadores de las dos fracciones:3 * 3 = 9.9 es el denominador de tu respuesta.ahora sabes que 2/3 * 7/3 = 14/9.

5. simplifica la fraccion.En este caso, como el numerador de la fracción es mayor que el denominador, sabemos que la fracción es mayor que 1 y debemos convertirla en un número mixto.(Un número mixto es un número entero con una fracción, como 1 2/3.)

6. Probemos con otro ejemplo!Supongamos que tenemos el siguiente problema 4/5 2/6 =.Primero, cambia el signo de división a un signo de multiplicación (4/5 * __ =), luego encuentra el recíproco de 2/6, que es 6/2.Ahora la tarea es la siguiente: 4/5 * 6/2 =__.ahora multiplicamos los numeradores, 4 * 6 = 24, y los denominadores 5* 2 = 10.Ahora tenemos lo siguiente:4/5 * 6/2 = 24/10.simplifica la fraccion. Como el numerador es mayor que el denominador, necesitaremos convertir esto a una fracción mixta.

7. Más información sobre la simplificación de fracciones. Es posible que hayas aprendido todo eso una vez, pero nunca está de más refrescar todo ese conocimiento perdido una vez más. Se pueden encontrar varios artículos en Internet para mejorar esas habilidades nuevamente.
Artículos sobre el tema. "Dividir fracciones por fracciones"
Оцените, пожалуйста статью
Popular