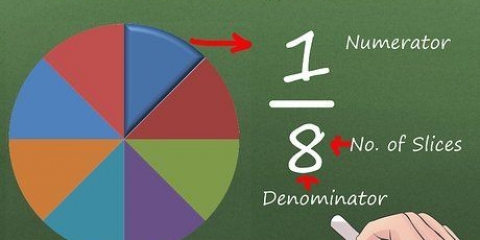
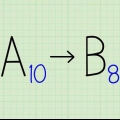Convertir de binario a decimal

Contenido

Pasos
Consejos

El sistema numérico decimal tiene diez valores posibles (0,1,2,3,4,5,6,7,8 o 9) para cada valor posicional. Esto contrasta con el sistema numérico binario que tiene solo dos valores posibles, a menudo representados por un 0 o un 1, para cada valor posicional. Para evitar confusiones al usar estos diferentes sistemas numéricos, la base de cada número individual a menudo se indica escribiéndola en subíndice. Por ejemplo, el número decimal 156 podría denotarse como 156₁₀ y se lee como "ciento cincuenta y seis, base diez". El número binario 10011100 se puede denotar como "base dos" escribiéndolo como 10011100₂. Dado que el sistema binario es el lenguaje interno de las computadoras electrónicas, los programadores serios deben saber cómo convertir decimales a binario y viceversa. Aquí está cómo hacer esto.

Pasos

Método 1 de 3: Elegir un método de conversión

División corta por dos con resto (fácil para principiantes).
Comparación con potencias decrecientes de dos y resta.

Método 2 de 3: Método uno: dividir por dos con resto

Este método es mucho más fácil de entender cuando se visualiza en papel. Sólo supone la división por dos.

Imagen titulada Convertir de decimal a binario Paso 1

1. Redacción del problema. En este ejemplo, tomemos el número decimal 156₁₀ convertir a binario.

Escribe el número decimal como el dividendo en forma invertida "división larga" símbolo.
Escriba la base del respectivo sistema (en nuestro caso "2" para binario) si el divisor está fuera de la curva del símbolo de división.

Imagen titulada Convertir de decimal a binario Paso 2

2. Escriba la respuesta entera (cociente) debajo del símbolo de división larga y escriba el resto (0 o 1) a la derecha del dividendo.

Básicamente, si el dividendo es un número par, el resto binario será 0; si el dividendo es impar el resto binario será 1.

Imagen titulada Convertir de decimal a binario Paso 3

3. Continuando hacia abajo, divida cada nuevo cociente por dos y escriba los restos a la derecha de cada dividendo. Detener cuando el cociente es 0.

Imagen titulada Convertir de decimal a binario Paso 4

4. Comenzando con el residuo inferior, lea la secuencia de residuos hacia arriba. Para este ejemplo, ahora debería tener 10011100. Este es el equivalente binario del número decimal 156. O, escrito con subíndice: 156₁₀ = 10011100₂

Este método se puede adaptar a decimales hasta cada notación para convertir. El divisor es 2 porque el formato deseado es. Si el resultado deseado es un formato diferente, reemplace el 2 en el método con el formato deseado. Por ejemplo, si el resultado deseado es la notación 9, reemplace 2 con 9. El resultado deseado estará entonces en el formato correcto.

Método 3 de 3: Método dos: Comparación con potencias decrecientes de dos y resta.

Imagen titulada Convertir de decimal a binario Paso 5

1. Escribe las potencias de dos en uno "sistema numérico binario" de derecha a izquierda. Comience en 2, evalúe como "1". Multiplica el exponente por 1 para cada potencia. La lista, hasta diez elementos, debería verse así. 512, 256, 128, 64, 32, 16, 8, 4, 2, 1

Imagen titulada Convertir de decimal a binario Paso 6

2. Encuentra la mayor potencia que se ajuste al número que deseas convertir a binario. En este ejemplo convertimos el número decimal 156₁₀ a binario. ¿Cuál es la mayor potencia que cabe en 156? Dado que cabe 128, escribimos un 1 como el dígito binario más a la izquierda y restamos 128 del número decimal, 156. ahora tienes 128.

Imagen titulada Convertir de decimal a binario Paso 7

3. Continuar a la siguiente potencia más baja de dos. Cabe 64 en 28? No, escribe un 0 antes del siguiente dígito binario a la derecha.

Imagen titulada Convertir de decimal a binario Paso 8

4. Cabe 32 en 28?No, entonces escribe un 0.

Imagen titulada Convertir de decimal a binario Paso 9

5. Cabe 16 en 28?Sí, entonces escribe un 1 y resta 16 de 28. ahora quedan 12.

Imagen titulada Convertir de decimal a binario Paso 10

6. Se adapta a 8 en 12?Sí, entonces escribe un 1 y resta 8 de 12. ahora te quedan 4.

Imagen titulada Convertir de decimal a binario Paso 11

7. Cabe 4 (potencia de dos) en 4 (decimal)?Sí, así que escribe un 1 y resta 4 de 4.Ahora queda 0.

Imagen titulada Convertir de decimal a binario Paso 12

8. Se adapta 2 en 0?No, entonces escribe un 0.

Imagen titulada Convertir de decimal a binario Paso 13

9. Cabe 1 en 0?No, entonces escribe un 0.

Imagen titulada Convertir de decimal a binario Paso 14

10. Componer la respuesta binaria. Como no hay más potencias de dos en la lista, has terminado. Ahora deberías tener 10011100. Este es el equivalente binario del número decimal 156. O, escrito con subíndice: 156₁₀ = 10011100₂

Repetir este método dará como resultado la memorización de las potencias de dos, lo que le permitirá omitir el paso 1.

Consejos

Convertir en la otra dirección, de binario a decimal, suele ser más fácil de aprender primero
práctica. Prueba el número decimal 178₁₀, 63₁₀ y 8₁₀ para convertir. Los equivalentes binarios son 10110010₂, 00111111₂ y 00001000₂.Prueba 209₁₀, 25₁₀ y 241₁₀ para convertir a, respectivamente, 11010001₂, 00011001₂, 11110001₂ Llegar.
La calculadora presente en su sistema operativo puede hacer esta conversión por usted. Pero como programador, es mejor que comprenda bien cómo funciona esta conversión. Las opciones de conversión de la calculadora se pueden hacer visibles en el menú "Estatua" > "Programador".