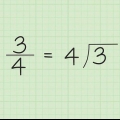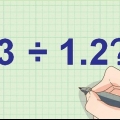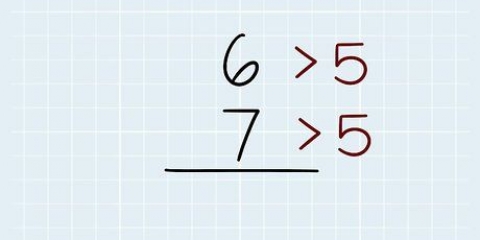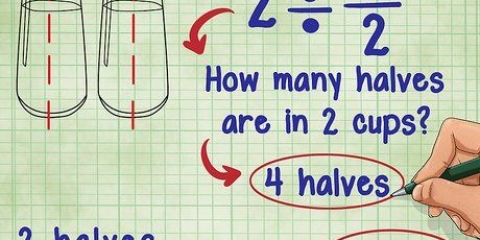En el ejercicio #1 (5厂65), 5 es el denominador y 6 es el primer dígito del numerador (65). 5 cabe en 6 una vez, así que pon un 1 en el signo de división, encima del 6. En el ejercicio #2 (3厂136), 3 (el divisor) no cabe completamente en 1 (el primer dígito del numerador). En este caso, escribe un 0 arriba del signo de división, arriba del 1. 
En el ejercicio #1 (5厂65), multiplica el número sobre la barra (1) por el denominador (5), lo que da como resultado 1 x 5 = 5, y coloque la respuesta (5) justo debajo de 6 de 65. En el ejercicio #2 (`3厂136) hay un cero encima del signo de división, así que si lo multiplicas por 3 (el denominador), el resultado es cero. Escriba un cero en una nueva línea justo debajo de 1 de 136. 
En el ejercicio #1 (5厂65), reste el 5 (el producto en la nueva fila) del 6 arriba (el primer dígito del numerador): 6 - 5 = 1. Coloque el resultado (1) en otra fila nueva directamente debajo de 5. En el ejercicio #2 (3厂136) resta el 0 (el producto en la nueva fila) del 1 en la parte superior derecha (el primer dígito en el contador). Coloque el resultado (1) en otra fila nueva directamente debajo del 0. 
En el ejercicio #1 (5厂65), baje el 5 de 65 para que quede junto al 1 obtenido al restar 5 de 6. Ahora hay 15 en esta fila. En el ejercicio #2 (3厂136), baja el 3 de 136 y colócalo al lado del 1, dándote 13. 
para continuar con 5厂65, divide el nuevo número (15) por 5 (el denominador), y escribe el resultado (3, porque 15 ÷ 5 = 3) a la derecha del 1 sobre el signo de división. Luego multiplicas este 3 arriba del signo de división por 5 (el denominador) y escribes el resultado (15, porque 3 x 5 = 15) menores de 15 años bajo el signo de división. Finalmente, reste 15 de 15 y escriba 0 en una nueva fila inferior. El problema de ejemplo #1 ahora está completo, ya que no hay más números para reducir en el denominador. La respuesta (13) está encima del signo de división. 
Para 3厂136: Determine cuántas veces 3 cabe completamente en 13 y escriba la respuesta (4) a la derecha del 0 sobre el signo de división. Luego multiplica 4 por 3 y escribe la respuesta (12) debajo de 13. Finalmente, reste 12 de 13 y escriba la respuesta (1) debajo de 12. 
Para 3厂136: Continuar el proceso para la siguiente ronda. Baje el 6 de 136, dejando 16 en la fila inferior. Divide 16 entre 3 y escribe el resultado (5) arriba del signo de división. Multiplica 5 por 3 y escribe el resultado (15) en una nueva fila inferior. Resta 15 de 16 y escribe el resultado (1) en una nueva fila inferior. Como no hay más dígitos para incluir en el numerador, ya terminó el problema y el 1 en la línea inferior es el resto (el número que queda). Escríbelo encima del signo de división, posiblemente con una `r`.`antes para que tu respuesta final` 45 r.1` se convierte. 

En este problema, 4 (el denominador) cabe en 5 (el primer dígito del numerador) una vez, con un resto de 1 (5 ÷ 4 = 1 r.1). Coloca el cociente, 1, sobre la línea de división larga. Coloque un pequeño superíndice 1 al lado del 5, para recordar que tenía un resto de 1. El 518 debajo de la línea de división ahora debería verse así: 518. 
En el problema, el número formado por el resto y el segundo número del numerador es 11. el denominador (4), entra en 11 dos veces, dejando un resto de 3 (11 ÷ 4 = 2 r.3) restos. Escribe el 2 arriba de la línea de división (dándote 12) y el 3 como un número en superíndice al lado del 1 en 518. El contador original, 518, ahora debería verse así: 518. 
En el problema, 38 es el siguiente (y último) número del numerador: el resto 3 del paso anterior y el número 8 es el último término del numerador. El denominador (4) cabe en 38 nueve veces con un resto de 2 (38 ÷ 4 = 9 r.2), porque 4x9 = 36, que es dos menos que 38. Escribe este último residuo (2) arriba de la línea de división para completar tu respuesta. Entonces tu última respuesta arriba del divisor es 129 r.2.. 

En este problema de ejemplo, invertiremos 5/8 para que el 8 esté en la parte superior y el 5 en la parte inferior. 
Por ejemplo: 3/4 x 8/5. 
En este caso, los numeradores son 3 y 8, y 3 x 8 = 24. 
Los denominadores son 4 y 5 en el problema, y 4x5 = 20. 
En la tarea: 3/4 x 8/5 = 24/20. 
En el caso de 24/20, 4 es el número más grande que va parejo en 24 y 20. Puedes confirmar esto escribiendo todos los divisores de ambos números y eligiendo el número más grande que sea divisor de ambos: 24: 1, 2, 3, 4, 6, 8, 12, 24 20: 1, 2, 4, 5, 10, 20 Como 4 es el máximo común divisor de 24 y 20, divide ambos números por 4 para simplificar la fracción. 24/4 = 6 20/4 = 5 24/20 = 6/5. Entonces: 3/4 5/8 = 6/5 
En el problema, 5 cabe en 6 una vez con un resto de 1. Entonces, el nuevo entero es 1, el nuevo numerador es 1 y el denominador sigue siendo 5. El resultado: 6/5 = 1 1/5. 

En la tarea: 8 - 5 = 3. 
Por lo tanto: 3 3 = 3. 

En el problema, todo lo que necesitas hacer es mover el punto decimal una posición tanto para el denominador como para el numerador. Entonces: 0.5 se convierte en 5 y 65.5 se convierte en 655. Sin embargo, si los números en el problema fueran 0.5 y 65.55, entonces moverías el punto decimal dos lugares en 65.55, convirtiéndolo en 6555. Como resultado, también debe cambiar el punto decimal en 0,5 dos lugares. Para hacer esto, agregue un cero al final y hágalo 50. 
En la declaración, el decimal viene en 655 después de los últimos 5 (como 655.0). Así que escribe el punto decimal arriba de la línea de división directamente arriba del punto decimal en 655. 
Divide la centésima (6) por 5. Entonces obtienes 1, con resto 1. Coloque 1 en el lugar centésimo en la parte superior de la línea de división larga y reste 5 de 6 debajo del número seis. El resto, 1, queda. Baje los primeros cinco en 655 y obtendrá el número 15. Divide 15 por 5 y obtienes 3. Coloque los tres sobre el carácter de división larga, al lado del 1. Bajar los últimos 5. Divide 5 por 5 y obtienes 1: coloca el 1 sobre el carácter de división larga. No hay resto, ya que 5 va una vez en 5. La respuesta es el número sobre el signo de división larga (131), entonces 655 5 = 131. Si saca una calculadora, verá que esta también es la respuesta a la división original: 65,5 0,5.
Hacer sumas de división
Contenido
La división es una de las cuatro operaciones aritméticas principales, junto con la suma, la resta y la multiplicación. Además de números enteros, también puedes dividir decimales, fracciones o exponentes. Puedes hacer una división larga o, si uno de los números es de un solo dígito, una división corta. Sin embargo, comienza a dominar la división larga, porque esa es la clave de toda la operación.
Pasos
Método 1 de 5: división larga

1. Escribe el problema usando unsigno de división larga. El signo de división larga ( 厂 ) parece un `paréntesis final` con un número debajo. Coloca el denominador, el número que estás dividiendo, fuera del signo de división larga, y el numerador, el número que estás dividiendo, dentro del signo de división larga .
- Problema de ejemplo #1 (principiante): 65 5. Coloca el 5 fuera de la división y el 65 dentro. debería verse como 5厂65, pero con el 65 debajo de la linea horizontal.
- Ejercicio de ejemplo #2 (avanzado): 136 3. Coloca el 3 fuera de la división y el 136 dentro de ella. debería verse como 3厂136, pero con el 136 debajo de la linea horizontal.

2. Divide la primera cifra del numerador por el denominador. En otras palabras, averigüe cuántas veces el denominador (el número fuera del signo de división) cabe en el primer dígito del numerador. Coloque el resultado entero encima del signo de división, justo encima del primer dígito del denominador.

3. Multiplica el número sobre el signo de división por el denominador. Toma el número que escribiste justo arriba de la división y multiplícalo por el denominador (el número a la izquierda de la división). Escriba el resultado en una nueva fila debajo del numerador, alineado con el primer dígito del numerador.

4. Resta el producto (resultado de la multiplicación) del primer dígito del numerador. En otras palabras, reste el número que acaba de escribir en la nueva línea debajo del numerador del número en el numerador directamente arriba. Escribe el resultado en una nueva fila, alineado debajo de los números de la resta.

5. Bajar el segundo dígito del contador. Baja el segundo dígito del contador a la nueva fila inferior, justo a la derecha del resultado de la resta que acabas de obtener.

6. Repita la división larga (tarea #1). Esta vez usa el numerador (el número a la izquierda del signo de división) y el nuevo número en la fila inferior (el resultado de tu primera ronda de matemáticas y el dígito que bajaste). Como antes, divide, multiplica y resta tus números para obtener el resultado.

7. Repita la división larga (tarea #2). Como antes, comienza con la división, la multiplicación y luego la resta.

8. Haz otra ronda de división larga y obtienes el resto (tarea #2). Cuando haya terminado con este problema, tenga en cuenta que hay un resto (es decir, un número sobrante al final de su cálculo). Pones este resto junto a tu respuesta completa.
Método 2 de 5: división corta

1. Use un guión para escribir el problema. Coloque el denominador, el número por el que está dividiendo, fuera (y a la izquierda) de la línea de división. Coloca el numerador, el número que vas a dividir, dentro (a la derecha y debajo) de la línea de división.
- A rápido para compartir, ¿Puede el denominador consistir en un solo dígito?.
- Asignación: 518 4. En este caso, el 4 estará fuera de la línea de división y el 518 estará dentro de ella.

2. Divide la primera cifra del numerador por el denominador. En otras palabras, determine cuántas veces el número fuera del divisor cabe en el primer dígito del número dentro del divisor. Escriba el número entero del resultado arriba de la barra de división y escriba cualquier resto en superíndice al lado del primer dígito del numerador.

3. Divida el resto y el segundo dígito del numerador por el denominador. Trate el número en superíndice que indica el resto como un dígito completo y combínelo con el dígito del numerador inmediatamente a la derecha. Determina cuántas veces el denominador entra completamente en este nuevo número de 2 dígitos y escribe el número entero y cualquier resto como lo hiciste antes.

4. Repite esto hasta que hayas pasado por todo el mostrador. Continúe determinando cuántas veces el denominador entra en el número formado por el siguiente dígito del numerador y el resto en superíndice inmediatamente a la izquierda del mismo. Una vez que haya pasado por todos los dígitos en el contador, tendrá su respuesta.
Método 3 de 5: dividir fracciones

1. Escribe la suma de la división para que las dos fracciones estén una al lado de la otra. A dividir fracciones, escribe la primera fracción seguida del símbolo de división (÷) y luego la segunda fracción.
- Por ejemplo, la declaración podría ser algo como: 3/4 5/8. Para mayor comodidad, use líneas horizontales en lugar de líneas diagonales para separar el numerador (número superior) y el denominador (número inferior) de cualquier fracción.

2. Invierta el numerador y el denominador de la segunda fracción. La segunda fracción se convierte en su propio inverso.

3. Cambiar la barra de división a un signo de multiplicación. Para dividir fracciones, se multiplica la primera fracción por el recíproco de la segunda.

4. Multiplica los numeradores de las fracciones. Sigue el mismo procedimiento que cuando multiplicas dos fracciones.

5. Multiplica los denominadores de las fracciones de la misma manera. De nuevo, esto es exactamente lo que harías para multiplicar dos fracciones.

6. Coloca el producto de los numeradores sobre el producto de los denominadores. Ahora que has multiplicado los numeradores y denominadores de ambas fracciones, puedes formar el producto de las dos fracciones.

7. Simplifica la fracción, si es necesario. Para simplificar la fracción, determinar el máximo común divisor, o el número más grande que cabe en ambos números en su totalidad, y luego divide tanto el numerador como el denominador por ese número.

8. Reescribe la fracción como un número mixto, si es necesario. Para hacer esto, divide el numerador por el denominador y escribe la respuesta como un número entero. El resto (el número que queda) es el numerador de la nueva fracción. El denominador de la fracción sigue siendo el mismo.
Método 4 de 5: dividir exponentes

1. Asegúrate de que los exponentes tengan la misma base. Usted puede dividir exponentes si tienen la misma base. Si no tienen la misma base, tendrás que manipularlos hasta que lo hagan, si puedes.
- Si recién estás comenzando con esto, primero haz un problema en el que ambos exponentes ya tengan la misma base. Por ejemplo: 3 3.

2. Restar los exponentes entre sí. Solo resta el segundo exponente del primero. No te preocupes por la base por ahora.

3. Coloca el nuevo exponente sobre la base original. Solo escribe el nuevo exponente sobre la base original. Eso es todo!
Método 5 de 5: dividir números decimales

1. Escribe el problema con un guión. Coloque el denominador, el número por el que está dividiendo, fuera (y a la izquierda) de la barra de división larga, y el numerador, el número por el que está dividiendo, dentro de la barra de división larga. A dividir decimales, convertir decimales a enteros primero.
- en el ejemplo 65,5 0,5 se coloca 0,5 fuera de la línea de división, y 65,5 dentro de ella.

2. Mueva los puntos decimales por igual para crear dos números enteros. Simplemente deslice los puntos decimales hacia la derecha hasta que estén al final de cada número. Asegúrate de moverlos la misma cantidad de posiciones para cada número; si necesitas mover el punto decimal dos lugares en el denominador, haz lo mismo con el numerador.

3. Coloque el punto decimal directamente encima de la línea de división. Coloque un decimal en el signo de división larga directamente encima del decimal en el numerador.

4. Resolver el problema realizando divisiones largas. Para dividir 655 entre 5, haz lo siguiente:
Artículos sobre el tema. "Hacer sumas de división"
Оцените, пожалуйста статью
Popular