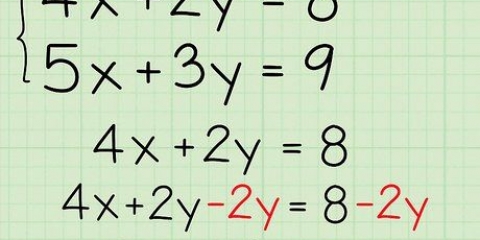ehmurciélagos metrosubir ocho Wcontracción nerviosa Vmultiplicar Dellen Ocontar asustraer El orden de las operaciones es importante en matemáticas, porque un orden incorrecto puede hacer que se encuentre una respuesta diferente. Por ejemplo, si tienes el problema 8 + 2 × 5 y primero sumas 2 a 8, obtienes 10 × 5=50 como respuesta. Pero si primero multiplicas 2 por 5, resulta que 8 + 10=18. solo la segunda respuesta es correcta. 
En una recta numérica, una versión negativa de un número está tan lejos de cero como lo está en el lado positivo, pero en la dirección opuesta. Sumar dos números negativos hace la suma más negativo (en otras palabras, los números se hacen más grandes, pero como el número es negativo, es un número más bajo). Dos signos negativos se anulan entre sí: restar un número negativo es lo mismo que sumar un número positivo. Multiplicar o dividir dos números negativos da una respuesta positiva. Multiplicar o dividir un número positivo y un número negativo da una respuesta negativa. 
Por ejemplo, para resolver la ecuación 9/3 - 5 + 3 × 4, arreglaríamos nuestro problema así: 

Por ejemplo, en la ecuación 2x + 3=11, x es la variable. Esto significa que hay algún valor que se puede sustituir por x para hacer que el lado izquierdo de la ecuación sea igual a 11. Como 2 × 4 + 3=11, en este caso x=4. Una manera fácil de entender las variables es reemplazarlas con un signo de interrogación en los problemas de álgebra. Por ejemplo: reescribe la ecuación 2 + 3 + x=9 como 2 + 3 + ?=9. Esto facilita ver cuál es el punto: necesitamos averiguar qué número agregar a 2 + 3 = 5 para obtener 9 como respuesta. la respuesta es de nuevo 4, naturalmente. 
Por ejemplo: mira la ecuación 2x + 1x=9. En este caso sumamos 2x y 1x para obtener 3x=9. Como 3 x 3=9, ahora sabemos que x=3. Tenga en cuenta nuevamente que solo puede agregar variables que son iguales. En la ecuación 2x + 1y=9, no podemos combinar 2x y 1y porque son dos variables diferentes. Esto también es cierto cuando una variable tiene un exponente diferente al de la otra. Por ejemplo, en la ecuación 2x + 3x=10, 2x y 3x no se pueden combinar porque las variables x tienen exponentes diferentes. Para obtener más información sobre cómo sumar exponentes, consulta wikiHow. 

En general, la suma y la resta son `opuestas`: una trabaja de la manera. Vea abajo: 
Con la multiplicación y la división, tienes que realizar la operación contraria en todo al otro lado del signo igual, incluso si es más de un número. Vea abajo: 
Esto puede ser un poco confuso, pero en estos casos se saca la raíz cuadrada de ambos lados cuando se trata de un exponente. Por otro lado, también tomas el exponente de ambos lados cuando se trata de una raíz cuadrada. Vea abajo: 

Por ejemplo: supongamos que tenemos un campo de fútbol que es 30 metros más largo que ancho. Usamos la ecuación l=w + 30 para representar esto. Podemos probar esta ecuación ingresando valores simples para w. Por ejemplo, si el campo tiene w = 10 metros de ancho, entonces tendrá 10 + 30 = 40 metros de largo. Si tiene 30 metros de ancho, entonces tendrá 30 + 30 = 60 metros de largo, etc. Esto parece lógico: esperamos que el campo se alargue a medida que se ensancha, por lo que esta ecuación parece una solución razonable. 
Por ejemplo, supongamos que redujimos una ecuación algebraica a x=1250. Si ingresamos 1250 en una calculadora, obtenemos una gran serie de decimales (debido a que la pantalla de la calculadora tiene un espacio limitado, no puede mostrar la respuesta completa). En este caso, podemos simplemente mostrar la respuesta como 1250 o simplificar la respuesta escribiéndola en notación científica. 
Factorizar ecuaciones de la forma ax + ba a a(x + b). Ejemplo: 2x + 4=2(x + 2) Factorización de ecuaciones de la forma ax + bx a cx((a/c)x + (b/c)) donde c es el número más grande que a y b encajan completamente. Ejemplo: 3y + 12y=3y(y + 4) Las ecuaciones de la forma x + bx + c se factorizan en (x + y)(x + z) donde y × z=c y yx + zx=bx. Ejemplo: x + 4x + 3=(x + 3)(x + 1). 

Si por alguna razón tu maestro no puede ayudarte, pregúntale sobre las opciones de tutoría en la escuela. Muchas escuelas tienen algún tipo de clases extra que te dan el tiempo extra y la atención que necesitas para sobresalir en álgebra. Recuerde que aprovechar la ayuda gratuita que está disponible no es motivo de vergüenza: es una indicación de que es lo suficientemente inteligente como para resolver sus problemas! 

Por ejemplo, en la ecuación 3 > 5x - 2, lo resolvemos de la misma forma que una ecuación normal: Esto implica que cualquier número menor que 1 es correcto para x. En otras palabras, x puede ser 0, -1, -2, etc. son. Si reemplazamos estos números en la ecuación de x, siempre obtenemos una respuesta menor que 3. 
Un ejemplo: resolver la fórmula cuadrática 3x + 2x -1=0. 
Por ejemplo: supongamos que estamos tratando con un sistema de ecuaciones y=3x - 2 y y=-x - 6. Si dibujamos estas dos líneas en un gráfico, obtenemos una línea que sube abruptamente y otra que desciende menos abruptamente. Como estas rectas se cortan en el punto (-1,-5), es que la solución del sistema. Si desea verificar esto, procese la respuesta en las ecuaciones del sistema: una buena respuesta debería `funcionar` para ambas ecuaciones. Ambas ecuaciones son `correctas`, por lo que nuestra respuesta es correcta!
Aprendiendo álgebra
Contenido
Aprender álgebra es importante para progresar con casi cualquier parte de las matemáticas en la educación secundaria y superior. Cada nivel de matemáticas se construye sobre la base, y con eso, cada nivel de matemáticas es particularmente importante. Sin embargo, incluso las habilidades matemáticas más básicas pueden ser difíciles de comprender para los principiantes cuando se enfrentan por primera vez. Si estás luchando con temas fundamentales de álgebra, no te preocupes. Con una pequeña explicación, algunos ejemplos simples y algunos consejos para mejorar tus habilidades, pronto serás un maestro del álgebra.
Pasos
Parte 1 de 5: Aprendiendo las reglas básicas del álgebra

1. Revisar las habilidades matemáticas básicas. Para aprender álgebra necesitarás conocer las habilidades básicas como suma, resta, multiplicación y división. Estas habilidades matemáticas que aprendes en la escuela primaria son esenciales antes de comenzar con el álgebra. Si no domina estas habilidades, será difícil aprender los conceptos más complejos que se tratan en álgebra. Si necesita un repaso de estas operaciones, consulte wikiHow para ver artículos sobre conceptos básicos de matemáticas.
- No es necesario ser muy bueno en aritmética mental si se quiere hacer bien el álgebra. A menudo se le permitirá trabajar con una calculadora durante la clase de matemáticas, para ahorrar tiempo mientras hace las sumas simples. En cualquier caso, debería poder hacer cálculos sin una calculadora, en caso de que no se le permita usarla.

2. Aprende el orden de las operaciones. Una de las cosas más difíciles cuando se trata de resolver una ecuación matemática es saber por dónde empezar. Afortunadamente, hay un cierto orden en el que resuelves estos problemas: primero los términos van entre paréntesis, luego los exponentes/potencias, luego la multiplicación, la división, la suma y finalmente la resta. Un mnemotécnico útil para recordar la secuencia de operaciones es, `¿Cómo deberíamos deshacernos de los insuficientes?` (o como un acrónimo HMWVDOA). Consulte wikiHow para obtener artículos sobre cómo aplicar el orden de las operaciones. Como recordatorio, aquí está nuevamente la secuencia de operaciones:

3. Aprende a usar números negativos. Es común en álgebra usar números negativos, por lo que es una buena idea repasar cómo sumar, restar, multiplicar y dividir números negativos antes de pasar al álgebra. A continuación, encontrarás algunos conceptos básicos para trabajar con números negativos que deberás recordar. Para obtener más información, consulta los artículos de wikiHow sobre sumas, restas, divisiones y multiplicaciones de números negativos.

4. Aprende a organizar problemas largos. Si bien los problemas de álgebra simples a menudo son fáciles de resolver, los problemas más complicados pueden requerir muchos pasos para completarse. Para evitar errores, comience en una nueva línea cada vez que esté un paso más adelante en la solución del problema. Si se trata de una ecuación con términos en dos lados del signo igual, intente escribir estos signos (`=`) uno debajo del otro. De esa forma, cualquier error en tu cálculo será mucho más fácil de detectar.
- 9/3 - 5 + 3×4
- 9/3 - 5 + 12
- 3 - 5 + 12
- 3 + 7
- 10
Parte 2 de 5: comprender las variables

1. Busque símbolos que no sean números. En álgebra, tendrás que lidiar con letras y símbolos en tus problemas matemáticos, en lugar de solo con números. Estas se llaman variables. Las variables no son tan difíciles como parecen a primera vista: son solo formas de representar números con valores desconocidos. A continuación se muestran algunos ejemplos comunes de variables en álgebra:
- Letras como x, y, z, a, b y c
- Letras griegas como theta o θ
- Tenga en cuenta que no todo los símbolos son variables desconocidas. Por ejemplo: pi o π, siempre es igual (redondeado hacia arriba) 3.1459.

2. Piense en las variables como números `desconocidos`. Como se mencionó anteriormente, las variables son generalmente solo números con valores desconocidos. En otras palabras, hay un número que puede tomar el lugar de la variable para hacer que la ecuación funcione. Por lo general, el objetivo de un problema de álgebra es descubrir cuál es esa variable; considéralo como un "número misterioso" que estás tratando de descubrir.

3. Si una variable aparece varias veces, simplifique las variables. ¿Qué haces cuando la misma variable aparece varias veces en una ecuación?? Si bien esto puede parecer una situación complicada, puede tratar las variables de la misma manera que lo haría con los números normales; en otras palabras, puede sumar, restar, etc. siempre y cuando solo combine variables que sean iguales. En otras palabras, x + x=2x, pero x + y no es igual a 2xy.
Parte 3 de 5: Resolver ecuaciones eliminando

1. Aislar la variable en la ecuación. Resolver una ecuación en álgebra generalmente implica tratar de determinar cuál es la variable. Las ecuaciones algebraicas suelen tener números y/o variables en ambos lados, así: x + 2=9 × 4. Para determinar cuál es la variable, tendrás que colocarla a un lado del signo igual. Lo que queda al otro lado del signo igual es la respuesta.
- En el ejemplo (x + 2=9 × 4), para aislar x del lado izquierdo de la ecuación, necesitamos deshacernos del `+ 2`. Para ello restamos 2 de este lado, quedando x=9 × 4. Para hacer que ambos lados de la ecuación sean iguales, también debemos restar 2 del otro lado. Esto nos deja con x=9 × 4 – 2. Según el orden de las operaciones, primero multiplicamos, luego restamos y obtenemos x=36 - 2=34.

2. Eliminar la suma por resta (y viceversa). Como vimos anteriormente, aislar x a un lado del signo igual generalmente implica tratar de deshacerse de los números inmediatamente adyacentes. Haces esto realizando la operación `opuesta` en ambos lados de la ecuación. Por ejemplo, en la ecuación x + 3=0, ponemos un `- 3` en ambos lados, porque hay un `+ 3` al lado de la x. Hacer esto aislará x y obtendrá `-3` al otro lado del signo igual, así: x=-3.
- Al sumar, restar. Ejemplo: x + 9=3 → x=3 - 9
- Al restar, sumar. Ejemplo: x - 4=20 → x=20 + 4

3. Elimina la multiplicación dividiendo (y viceversa). La multiplicación y la división son un poco más difíciles de trabajar que la suma y la resta, pero tienen la misma relación "opuesta". Si ves un `×3` en un lado, puedes eliminarlo dividiendo ambos lados por 3.
- Al multiplicar, dividir. Ejemplo: 6x=14 + 2→ x=(14 + 2)/6
- Al dividir, multiplicar. Ejemplo: x/5=25 → x=25 × 5

4. Eliminar exponentes sacando raíces cuadradas (y viceversa). Los exponentes son un tema avanzado en álgebra. Si no sabes qué hacer con ellos, lee el artículo de wikiHow para principiantes sobre exponentes. El `opuesto` de un exponente es la raíz a la potencia de ese número. Por ejemplo, el opuesto del exponente es la raíz cuadrada (√), el opuesto del exponente es la raíz cúbica (√), etc.
- Para exponentes, saca la raíz cuadrada. Ejemplo: x=49 → x=√49
- Para las raíces, tome el exponente. Ejemplo: √x=12 → x=12
Parte 4 de 5: Mejora tus habilidades matemáticas

1. Usa imágenes para aclarar los problemas. Si no puede representar un problema de álgebra, use gráficos o imágenes para ilustrar la ecuación. Incluso puedes usar un grupo de objetos (como bloques o monedas) si los tienes a mano.
- Por ejemplo, resolvamos la ecuación x + 2=3 usando cajas (☐)
- x+2=3
- ☒+☐☐=☐☐☐
- En este punto, resta 2 de ambos lados quitando 2 cuadrados (☐☐) de cada lado:
- ☒+☐☐-☐☐=☐☐☐-☐☐
- ☒=☐, o x=1
- Otro ejemplo: 2x=4
- =☐☐☐☐
- En este punto, dividimos ambos lados por dos, dividiendo las cajas de ambos lados en dos grupos:
- ☒|☒=☐☐|☐☐
- ☒=☐☐, o x=2

2. Use `verificaciones lógicas` (especialmente cuando se trata de problemas). Cuando necesite convertir un problema en una ecuación algebraica, verifique su fórmula procesando valores simples en las variables. ¿Tu ecuación es correcta cuando x=0?? Cuando x=1? Cuando x=-1? Es fácil cometer pequeños errores al anotar algo como p=6d cuando te refieres a p=d/6, pero los detectarás lo suficientemente rápido si revisas el trabajo que has hecho antes de continuar.

3. Tenga en cuenta que las respuestas no siempre son números enteros en matemáticas. Las respuestas en álgebra y otras ramas de las matemáticas no siempre son números redondos y fáciles. A menudo son decimales, fracciones o números irracionales. Una calculadora puede ayudarte a encontrar estas respuestas complicadas, pero ten en cuenta que tu maestro puede pedirte que des la respuesta exacta y no en un decimal torpe.

4. Si está familiarizado con los conceptos básicos de álgebra, intente factorizar. Una de las habilidades más complicadas del álgebra es la factorización, una especie de atajo para escribir ecuaciones complejas en una forma más simple. La factorización es un tema bastante avanzado en álgebra, así que consulte el artículo vinculado anteriormente si le resulta difícil. Aquí hay algunos consejos para ayudar a factorizar ecuaciones:

5. Práctica práctica práctica! La progresión en el aprendizaje del álgebra (y cualquier otra rama de las matemáticas) requiere mucho trabajo duro y repetición. No te preocupes: si prestas atención en clase, haces todas tus tareas y pides ayuda a tu maestro o a otros estudiantes cuando sea necesario, el álgebra eventualmente se convertirá en una segunda naturaleza.

6. Pídele a tu profesor que te ayude con las materias más difíciles. Si tiene dificultades para dominar el material, no se preocupe, no tiene que aprenderlo por su cuenta. Tu profesor es la primera persona que te ayuda con las preguntas. Después de clase, pídele ayuda educadamente al profesor. Los buenos profesores generalmente están dispuestos a volver a explicar un tema cuando los visitas después de clase, e incluso pueden proporcionarte material de práctica adicional.
Parte 5 de 5: Exploración de temas avanzados

1. Aprende a graficar una ecuación. Los gráficos son herramientas valiosas en álgebra porque le permiten representar ideas que generalmente requieren números en imágenes fáciles de entender. Por lo general, cuando comienza con álgebra, los gráficos se limitan a problemas de ecuaciones con dos variables (generalmente x e y) y se representan en un gráfico bidimensional simple con un eje x y un eje y. Con estas ecuaciones, todo lo que tiene que hacer es ingresar un valor para x, luego resolver para y (o viceversa) para obtener dos números que correspondan a un punto en el gráfico.
- Por ejemplo, en la ecuación y=3x, sustituimos 2 por x, y obtenemos y=6 como respuesta. Esto significa que el punto (2.6) (dos puntos a la derecha del punto cero y 6 arriba) es parte de la gráfica de la ecuación.
- Las ecuaciones de la forma y=mx + b (donde m y b son números) son especial solo dentro de los conceptos básicos de álgebra. Estas ecuaciones siempre tienen pendiente m y se cruzan con el eje y en el punto y=b.

2. Aprende a resolver desigualdades. ¿Qué haces cuando una ecuación no tiene un signo igual?? Nada especial en comparación con lo que harías de otra manera, resulta. En desigualdades, donde encuentras signos como, > (`mayor que`) y< (`menor que`), resuelve la ecuación de la misma manera que antes. La respuesta que obtienes es más pequeña o más grande que tu variable.
- 3 > 5x - 2
- 5 > 5x
- 1 > x, o X< 1.

3. Resolver ecuaciones cuadráticas o cuadráticas. Un tema algebraico con el que tropiezan muchos principiantes es resolver ecuaciones cuadráticas. Estas son ecuaciones de la forma ax + bx + c=0, donde a, b y c son números (excepto que a no puede ser 0). Resolvemos estas ecuaciones con la fórmula x=[-b +/- √(b - 4ac)]/2a . Tenga cuidado: el +/- significa que tiene que encontrar las respuestas para ambas sumas Si restar, de modo que haya dos respuestas posibles para este tipo de problema.
- x=[-b +/- √(b - 4ac)]/2a
- x=[-2 +/- √(2 - 4(3)(-1))]/2(3)
- x=[-2 +/- √(4 - (-12))]/6
- x=[-2 +/- √(16)]/6
- x=[-2 +/- 4]/6
- x=-1 y 1/3

4. Experimentar con el sistema de ecuaciones. Resolver múltiples ecuaciones a la vez puede sonar muy complicado, pero si estás trabajando con ecuaciones algebraicas simples, no es tan difícil. A menudo, los profesores de matemáticas usan un gráfico para resolver estos problemas. Si trabajas con sistemas de dos ecuaciones, encontrarás la solución mirando los puntos de la gráfica donde se cruzan las rectas de ambas ecuaciones.
- y=3x - 2
- -5=3(-1) - 2
- -5=-3 - 2
- -5=-5
- y=-x - 6
- -5=-(-1) - 6
- -5=1 - 6
- -5=-5
Consejos
- Hay toneladas de recursos para las personas que quieren aprender álgebra en línea. Solo una simple búsqueda en un motor de búsqueda como `ayuda de álgebra` puede dar docenas de excelentes resultados. También eche un vistazo a la categoría Matemáticas. Allí encontrará mucha información, así que comience de inmediato!
- Un gran sitio para principiantes de álgebra es khanacademy.com. Este sitio gratuito ofrece muchas lecciones fáciles de seguir sobre una gran variedad de temas, incluido el álgebra. Hay videos sobre todo, desde temas extremadamente básicos hasta temas de nivel universitario, así que no dude en aprovechar Khan Academy y toda la ayuda que este sitio puede brindarle!
- Recuerda que los mejores recursos para aprender álgebra son las personas que ya conoces. Consulte con amigos u otros estudiantes en la misma clase si necesita ayuda con los temas tratados en clase.
Artículos sobre el tema. "Aprendiendo álgebra"
Оцените, пожалуйста статью
Popular