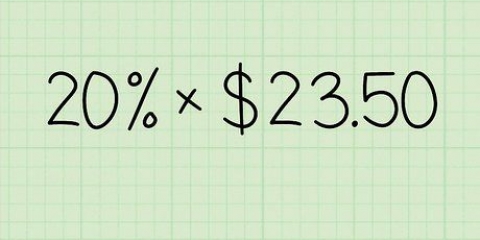En este caso no sabemos cuál es el porcentaje. Sabemos que 40 € es la cantidad anterior y 32 € es la cantidad nueva. 
En este ejemplo, escribiría 32, luego presionaría el botón dividir, luego escribiría 40, luego presionaría el signo igual. La respuesta: 0.8 (Esta no es la respuesta final). 

Dado que el precio del ejemplo ha bajado y el precio que calculamos también es un descuento, estamos en el camino correcto. Sin embargo, si el precio en el ejemplo ha bajado de $40 a $32 y obtuvimos un 120 % después del cálculo, entonces sabemos que algo salió mal porque esperábamos un descuento y no un aumento. 

Tarea 1: Una blusa de 50€ ahora cuesta 28€. ¿Cuál es el porcentaje de descuento?? Resuelve esto con una calculadora. Ingrese `28`, presione el botón `dividir`, ingrese `50`, presione el signo igual; la respuesta es 0.56. Convertir `0.56` en `56%`. Compare este número con el 100 %, restando `56` de `100`. Esto da un descuento del 44%. Tarea 2: Una gorra de béisbol de 12 € cuesta 15 € después del IVA. ¿Cuál fue el porcentaje de IVA?? Resuelve esto con una calculadora. Escriba `15`, presione el botón `compartir`, escriba `12`, presione el signo igual; la respuesta es 1.25. Convertir `1.25` a `125%`. Compare esto con el 100 % restando `100` de `125`, lo que da un aumento del 25 %. 




Por ejemplo, 67% se convierte en 0,67; 125% se convierte en 1,25; 108% se convierte en 1.08, etc. Divide el porcentaje por 100 y omite el porcentaje. Expresa el porcentaje como un decimal. 
25 x 0,40 = ? Recuerda que restamos el precio de descuento (60%) de 100, lo que nos deja un 40% y lo convertimos a decimal. 
25 x 0,40 = ? Multiplica estos dos números y obtienes `10`. Pero `10` qué? 10 euros por supuesto, así que sabemos que los nuevos vaqueros solo costarán 10 euros después del 60% de descuento. 
Tarea 1: Se venden vaqueros de 120€ con un 65% de descuento. Cuál es el precio de venta? Solución: 100 - 65 = 35; 35% convertir a 0,35. 0,35 x 120 = 42; el nuevo precio es de 42€ (una ganga!) Tarea 2: Una colonia de 4800 bacterias crece un 20%. cuantas bacterias hay? Solución: 100 + 20 = 120; 120% se puede convertir a 1.2. 1,2 x 4800 = 5760; ahora hay 5760 bacterias en la colonia. 

Supongamos que tenemos que resolver el siguiente problema: Un video está a la venta con un 75% de descuento. El precio de venta es de 15€. Cuál era el precio original? Con un descuento tenemos que lidiar con una caída en el precio. 15€ es el `nuevo importe`, porque este es el importe después de aplicar el descuento. 
Debido a que estamos lidiando con una disminución/descuento aquí, hacemos 100 – 75 = 25 %. 
25% luego se convierte en 0.25. 

Tome una calculadora y presione `15`, presione dividir y presione `0.25` y luego presione el signo igual. 
15 dividido por 0,25 = 60, lo que significa que el precio anterior era de $60. Si desea volver a verificar la respuesta para asegurarse de que sea correcta, multiplique el precio de venta (75 % o 0,75) por el precio anterior ($60) y verifique que obtiene el precio de venta como resultado.
(15 €): 0,75 x 60 = 45 € de descuento; 60 € (precio antiguo) - 45 € (rebaja) = 15 € (precio rebaja) 
Esto es un aumento, entonces 100 + 22. Convierta la respuesta a un decimal: 122% se convierte en 1,22 Usando una calculadora, presione `1525`, divida, `1.22` y luego el signo igual. Dar a la respuesta una unidad apropiada. Con este enunciado (1525/1,22 = 1250), la inversión original es por tanto de 1250€.
Cálculo con porcentaje de aumento o disminución
Contenido
Es posible que esté tratando de responder una pregunta como `Si una blusa de $45 tiene un 20 % de descuento, ¿cuál es el precio de descuento??Este tipo de preguntas también se denominan preguntas sobre porcentaje de aumento/disminución, y son una parte bastante fácil de las matemáticas. Con un poco de ayuda, puede resolverlos fácilmente y puede hacerlos rápidamente mientras duerme.
Pasos
Método 1 de 3: Cálculo del porcentaje

1. Utilice este método cuando se desconozca el porcentaje, como en los siguientes ejemplos:Si una camiseta de 40 € ahora se vende por 32 €, ¿cuál es el porcentaje de descuento??

2. Decida qué valor es el monto original o anterior, y qué monto se descuenta. La cantidad después de tomar el porcentaje se llama `nueva cantidad`.

3. Divida la nueva cantidad por la cantidad anterior.Asegúrese de ingresar primero la cantidad anterior en la calculadora.

4. Mueva el punto decimal dos lugares a la derecha para convertir el decimal en un porcentaje. En este ejemplo, 0.8 cambia a 80%.

5. Compara el porcentaje con el 100%. Si su respuesta es menor al 100%, entonces hay una disminución o descuento; si el porcentaje es superior al 100%, entonces se trata de un aumento (de precio).

6. Compara tu porcentaje con el 100%. Averigüe cuánto está por encima o por debajo del 100%, y entonces sabrá esta la respuesta final es. En nuestro ejemplo, el 80 % comparado con el 100 % es un 20 % de descuento.

7. Practica con los siguientes ejemplos. Para obtener más información, consulte los siguientes problemas y vea si sabe cómo resolverlos:
Método 2 de 3: calcular el nuevo valor

1. Utilice este método cuando se desconozca el nuevo valor, como en los siguientes ejemplos:Los vaqueros de 25€ tienen un 60% de descuento. ¿Cuál es el nuevo precio de los pantalones?? o Una colonia de 4800 bacterias crece un 20%. cuantas bacterias hay?

2. Determine si se trata de un aumento o una disminución. Por ejemplo, algo como el IVA es un aumento. Sin embargo, un descuento es una disminución.

3. Si se trata de un aumento, sume el porcentaje a 100. Entonces, un 8% de IVA equivale al 108%, o un recargo del 12% da un total de 112%.

4. Si se trata de una disminución, reste el porcentaje de 100. Si algo tiene un descuento del 30%, hay que pagar el 70%; un descuento del 12% indica que te quedas con el 88%.

5. Convierta la respuesta del Paso 3 o Paso 4 a un número decimal. Esto significa que mueves el punto decimal dos lugares a la izquierda.

6. Multiplique este decimal por la cantidad original. Supongamos que se trata del siguiente problema: Los vaqueros de 25€ tienen un 60% de descuento. ¿Cuál es el precio de descuento?? Puedes resolver esto de la siguiente manera:

7. Marque la subida o bajada correctamente y listo. En el ejemplo anterior teníamos:

8. Practique en los siguientes ejercicios de muestra. Para comprender mejor este problema, repase los siguientes ejercicios y vea si puede resolverlos:
Método 3 de 3: calcular la cantidad original

1. Si no conoce la cantidad original, use el siguiente método, como en los siguientes ejemplos:Un videojuego está en oferta con un 75% de descuento. El precio de venta es de 15€. Cuál era el precio original? o Una inversión ha crecido un 22% y ahora vale 1525€. ¿Cuánto se ha invertido en principio??
- Para poder resolver estas preguntas, debes entender que los porcentajes se aplican multiplicando. Ya sea un aumento o una disminución, es una multiplicación. Tu trabajo es deshacer la multiplicación. Tú haces el ascenso o la caída no deshecho, pero el porcentaje. Por lo tanto, tres cosas se aplican aquí:
- jeje dividido por el porcentaje.
- Si se trata de un aumento, entonces sumas el porcentaje a 100.
- Si se trata de una disminución, se resta el porcentaje de 100.

2. Determinar si es un aumento o una disminución. el IVA, por ejemplo, es un aumento; el descuento es una disminución. Una inversión que sube de valor es un aumento; una población que disminuye en número es una disminución, y así sucesivamente.

3. Si es un aumento, sume el porcentaje a 100. Si es una disminución, reste el porcentaje de 100.

4. Convertir ese valor a decimal. Esto se hace moviendo el punto decimal dos lugares a la izquierda o dividiendo el número por 100.

5. Divide la `nueva cantidad` por el decimal del paso 3. Esto invierte la multiplicación de la que hablamos en el paso 1.

6. Nuestro `nuevo importe` es de 15€, y el decimal es 0,25.

7. Dale a todo el nombre correcto y listo. Ahora ha calculado el precio anterior.

8. Practica con los siguientes ejemplos. Para comprender mejor este tipo de problema, lea los problemas e intente completar los problemas: Una inversión ha crecido un 22% y ahora vale 1525€. ¿Cuánto invirtió originalmente??
Consejos
- no olvides la coma.
- Si no sabes cuál es la nueva cantidad, tienes que multiplicar. De lo contrario, tienes que compartir.
- Si es un aumento, sume el porcentaje a 100; si es una disminución, reste el porcentaje de 100. Esto es cierto ya sea que vayas a multiplicar o dividir.
- No olvides las unidades (Euros, Dólares, Libras, Porcentaje, etc.)..). Tenga en cuenta que omitir unidades puede costarle puntos en una prueba.
- Trate de estimar. Calcula aproximadamente cuál será tu respuesta (más de 100? 200? Menos de 50? 20?) y verifique sus cálculos para ver si acertó.
Advertencias
- El orden de las operaciones en asuntos de división! Asegúrese de ingresar primero el número correcto en la calculadora.
Artículos de primera necesidad
- Una calculadora
- Papel
Artículos sobre el tema. "Cálculo con porcentaje de aumento o disminución"
Оцените, пожалуйста статью
Popular