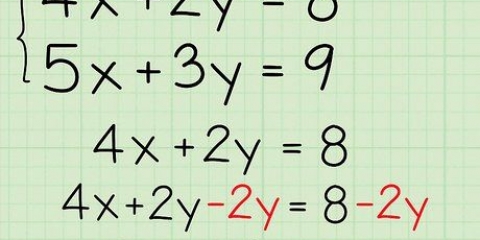Cómo integrar: 9 pasos (con fotos)

Contenido

Pasos
- Método 1 de 2: fácil integración
- Método 2 de 2: otras reglas

La integración es el reverso de la diferenciación dentro de las matemáticas (análisis). Es el proceso de calcular el área bajo una curva encerrada por un plano xy. Hay diferentes reglas para integrar según el tipo de polinomio (polinomio) con el que estés tratando.

Pasos

Método 1 de 2: fácil integración

1. La siguiente regla de integración simple funciona para casi todos los polinomios estándar. Toma el polinomio y = a*x^n.

2. Divide a (el coeficiente) por n+1 (la potencia + 1) y aumenta la potencia en 1. En otras palabras, la integral de y = a*x^n es y = (a/n+1)*x^(n+1).

3. Agregue la constante de la integral C para integrales desconocidas, para corregir su significado inherente con respecto al valor exacto. Por lo tanto, la respuesta final en este caso es y = (a/n+1)*x^(n+1) + C.

Piénsalo de esta manera: cuando calculas la derivada de una función, las constantes simplemente se omiten de la respuesta final. Por lo tanto, siempre es posible que la integral de una función tenga una constante arbitraria.

4. Integrar partes separadas de una función con la regla. Por ejemplo, la integral de y = 4x^3 + 5x^2 +3x es (4/4)x^4 + (5/3)*x^3 + (3/2)*x^2 + C = x^4 + (5/3)*x^3 + (3/2)*x^2 + C.

Método 2 de 2: otras reglas

1. Las mismas reglas no se aplican a x^-1, o 1/x. Cuando integras una variable elevada a la potencia -1, la integral es de logaritmo natural de la variable. En otras palabras, la integral de (x+3)^-1 es ln(x+3) + C.

2. La integral de e^x siempre es igual a sí misma. La integral de e^(nx) es 1/n * e^(nx) + C; por tanto, la integral de e^(4x) es igual a 1/4 * e^(4x) + C.

3. Integrar funciones trigonométricas requiere aprender ciertas integrales. Recuerda las siguientes integrales:

La integral de cos(x) es sen(x) + C.

La integral de sin(x) es -cos(x) + C. (tenga en cuenta el signo menos!)

Con estas dos reglas puedes calcular la integral de tan(x), que es equivalente a sin(x)/cos(x). La respuesta es -ln|cos x| + C - revisa tu trabajo!

4. Con polinomios más complejos como (3x-5)^4, tendrás que aprender a integrar por sustitución. Esta técnica introduce una variable, como la letra u, que representa un polinomio de variables, como 3x-5, para simplificar el proceso sin dejar de aplicar las mismas reglas para integrar.