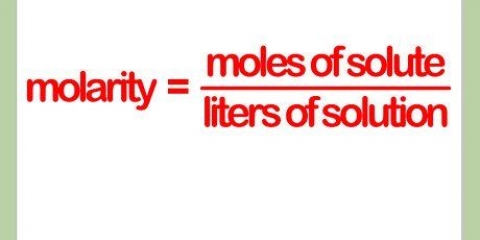Calcular la corrección del factor de potencia: 8 pasos (con fotos)

Contenido

Pasos
Advertencias
Artículos de primera necesidad

A través de la corrección del factor de potencia se puede calcular la potencia aparente, la potencia, la potencia reactiva y el ángulo de fase. Considere la ecuación de un triángulo rectángulo. Para calcular un ángulo necesitas saber cuál es el coseno, el seno y la tangente. También debes usar el teorema de Pitágoras (c² = a² + b²) para calcular las dimensiones de los lados del triángulo. También necesitas saber qué unidades tiene cada tipo de habilidad. La potencia aparente se mide en voltios-amperios. La potencia se mide en vatios y la potencia reactiva se expresa en unidades de voltios-amperios reactivos (VAR). Hay varias ecuaciones para calcularlas y todas se tratarán en este artículo. Ahora tiene la base de lo que está tratando de calcular.

Pasos

Imagen titulada Calcular la corrección del factor de potencia Paso 1

1. Calcular la impedancia. (Imagínese que la impedancia está en el mismo lugar que la potencia aparente en la imagen de arriba). Para determinar la impedancia usas el teorema de Pitágoras,c² = √ (a² + b²).

Imagen titulada Calcular la corrección del factor de potencia Paso 2

2. Por lo tanto, la impedancia total (representada como `Z`) es igual a la potencia al cuadrado, más la potencia reactiva al cuadrado, luego saca la raíz cuadrada de la respuesta.

(Z = √(60² + 60²)). Entonces, si ingresa eso en su calculadora científica, la respuesta es 84.85Ω. (Z = 84,85 Ω).

Imagen titulada Calcular la corrección del factor de potencia Paso 3

3. Determinar el ángulo de fase. Entonces ahora tienes la hipotenusa, que es la impedancia. También tienes un lado adyacente, la potencia, y tienes el lado opuesto, la potencia reactiva. Entonces, para encontrar el ángulo, puede usar una de las fórmulas mencionadas anteriormente. Por ejemplo, usamos la fórmula de la tangente, es decir, el lado opuesto dividido por el adyacente (reactivo/potencia).

Entonces tienes una ecuación como: (60/60 = 1)

Imagen titulada Calcular la corrección del factor de potencia Paso 4

4. Tome el recíproco de la tangente para el ángulo de fase. La tangente inversa es un botón en tu calculadora. Así que ahora toma la tangente inversa de la ecuación en el paso anterior y obtienes el ángulo de fase. Tu ecuación debería verse así: tan ‾ ¹ (1) = ángulo de fase. su respuesta será entonces 45°.

Imagen titulada Calcular corrección del factor de potencia Paso 5

5. Calcular la corriente total (Amperios). La corriente también se muestra como una `A` en la unidad Ampere. La fórmula utilizada para calcular la corriente es el voltaje dividido por la impedancia, así que esto es: 120V/84.85Ω. Ahora tiene una respuesta de aproximadamente 1.141A. (120 V/84,84 Ω = 1,141 A).

Imagen titulada Calcular la corrección del factor de potencia Paso 6

6. Ahora necesita calcular la potencia aparente que se muestra como `S`. No necesitas usar el teorema de Pitágoras para calcular la potencia aparente porque tu hipotenusa se considera tu impedancia. Recuerde que la potencia aparente utiliza la unidad Voltio-Amperio: podemos calcular la potencia aparente mediante la fórmula: Voltaje al cuadrado dividido por la impedancia total. Su ecuación debería verse así: 120V²/84.85Ω. Ahora debería obtener una respuesta como: 169.71VA. (120²/84,85 = 169,71).

Imagen titulada Calcular la corrección del factor de potencia Paso 7

7. Ahora necesita calcular la potencia que se muestra como `P`. Para calcular la potencia necesitas la corriente como lo hiciste en el paso cuatro. La potencia está en Watts y se calcula multiplicando la corriente al cuadrado (1.141²) por la resistencia (60Ω) en su circuito. Debería obtener una respuesta de 78.11 vatios. La ecuación debería verse así: 1.141² x 60 = 78.11.

Imagen titulada Calcular la corrección del factor de potencia Paso 8

8. Calcular la potencia o factor de potencia! Para calcular el factor de potencia necesitas la siguiente información: Watts y Volt-Amps. Usted calculó esta información en los pasos anteriores. La potencia es igual a 78.11W y Volt-Amperio es 169.71VA. La fórmula para el factor de potencia, también representada como Pf, es vatios divididos por voltios-amperios. Su ecuación ahora se ve así: 78.11/169.71 = 0.460.

Esto también se puede expresar como un porcentaje, por lo que se multiplica 0,460 por 100, lo que da un factor de potencia del 46 %.

Advertencias

Al calcular la impedancia, usa la función de tangente inversa y no solo la función de tangente regular en su calculadora. De lo contrario obtendrá un ángulo de fase incorrecto.
Este fue solo un ejemplo muy simple de calcular un ángulo de fase y un factor de potencia. Hay circuitos mucho más complicados, que incluyen potencia de capacitancia y resistencias e impedancia más altas.