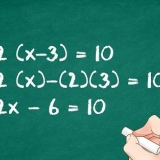Convertir unidades

Contenido

Pasos
Consejos

Con todos los diferentes sistemas de medidas que existen en el mundo, puede ser útil poder convertir unidades. Esto es fácil dentro del sistema métrico, pero si estás trabajando con el sistema imperial, tendrás que ser capaz de trabajar con fracciones. Independientemente del sistema que utilice, siempre tendrá que tener cuidado con las unidades en cada paso del camino para realizar un seguimiento de dónde se encuentra.

Pasos

Método 1 de 3: conversión de unidades

1. Compara las dos unidades. Las dos unidades deben medir lo mismo. Supongamos que tiene un problema como `Convertir 2 pulgadas a centímetros, entonces tanto las pulgadas como los centímetros son unidades de longitud. Si sus unidades miden dos cosas diferentes (como altura y peso), no puede convertirlas entre sí.

La gente a menudo se confunde acerca de la longitud, el área y el volumen, que indican tres cosas diferentes. Recuerda que `cuadrado` o `` significa área, y `cúbico` o `` significa volumen.
También puedes escribir este ejemplo como 2 pulgadas =? cm.

2. Descubra qué factor de conversión debe utilizar. Antes de que pueda comenzar a calcular, necesita saber cuánto más grande es una unidad en comparación con la otra. Si la conversión que encontró contiene muchos decimales, luego redondearlo al dígito significativo más cercano. Si no sabe qué es un dígito significativo, redondee al segundo o tercer decimal.

Por ejemplo, si desea convertir 2 pulgadas a centímetros, necesita saber que 1 pulgada = 2,54 centímetros.

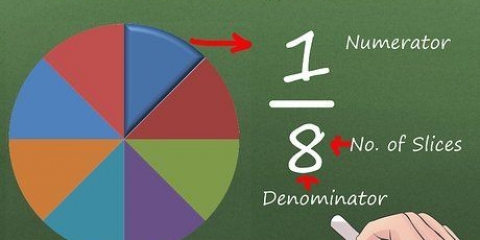
3. Escribe la conversión como una fracción. Escribe esta conversión como una fracción, con la unidad. Coloque la unidad con la que comienza debajo (el denominador) y la unidad en la que para convertirarriba (el mostrador).

Por ejemplo, escribe /_{1 pulgada}. Puedes leer esto como "2,54 centímetros por pulgada".

4. Multiplica tu número original por la fracción. Multiplicar estos dos números te da la respuesta. Para empezar, primero escribe la multiplicación, con las unidades después de cada valor.

2 pulgadas x /_{1 pulgada} = ?

5. Resuelve la multiplicación. Es importante realizar un seguimiento de las unidades mientras se hace esto. Cada unidad en la ecuación aún debe estar allí durante cada paso.

2 pulgadas x /_{1 pulgada}

= /_{1 pulgada}

= /_pulgada

6. Eliminar unidades del numerador y denominador. Si la misma unidad está en el numerador y en el denominador de la fracción, táchala. lo que te queda es tu respuesta.

/_pulgada

= 5,08cm.

7. corregir errores. Si no puede deshacerse de las unidades, comience desde cero y vuelva a intentarlo. Tal vez pusiste la mitad equivocada de la fracción en el numerador.

Por ejemplo, si calculó 2 pulgadas x (1 pulgada/2,54 cm), su respuesta se dará con las unidades "pulgada x pulgada/cm", lo cual no tiene ningún significado. Las pulgadas funcionarán si inviertes la fracción, así como 2 pulgadas x (2,54 cm / 1 pulgada).

Método 2 de 3: convertir valores de varias unidades

1. Tenga en cuenta la tarea. Trate de averiguar exactamente qué está preguntando el problema y escríbalo como un problema de matemáticas. Aquí hay un ejemplo:

Si una bicicleta se mueve a 10 millas por hora, ¿cuántos pies recorres en un minuto??
Escriba esto como `10 millas/hora =? pie/minuto` o `10 millas/hora =? pie / min`.

2. Determine la conversión para una unidad. Recuerda, solo puedes convertir entre dos mismas unidades de medida. En nuestro ejemplo tenemos unidades para la longitud (millas y pies) y unidades que miden el tiempo (horas y minutos). Comience con un par y determine la conversión.

Por ejemplo, 1 milla = 5280 pies.

3. Multiplica el número por la fracción de la conversión. Tal como se describe en la sección anterior, podemos escribir la conversión como una fracción, para cancelar unidades. Asegúrese de que cada unidad esté presente en sus cálculos.

/ _Uds)X/ _millas

= / _{x millas}

4. Elimina las unidades. Una de las unidades está en el numerador y la otra en el denominador para que puedas deshacerte de ellas. Sin embargo, aún no estás listo, pero estás más cerca de la respuesta.

/ _{tú x millas}

= / _Uds

5. Multiplique de la misma manera por otro factor de conversión. Seleccione una unidad que no haya sido convertida y escriba la conversión como una fracción. Recuerda escribir la fracción de modo que las unidades se anulen entre sí durante la multiplicación.

En nuestro ejemplo, todavía necesitamos convertir de horas a minutos. 1 hora = 60 minutos.

Ahora mismo tenemos 52800 pies/hora. Como el número de horas está en el denominador, queremos que la nueva fracción tenga las horas en el numerador: 1 hora/60 minutos.

/ _Uds X/ _{60 minutos}

= / _{h x min}

6. Elimina las unidades. Otra unidad tendrá que ser eliminada, al igual que antes.

/ _{Uds x min}

= / _min

7. Sigue repitiendo esto hasta que se complete la conversión. Si tu respuesta está en las unidades a las que querías convertir, entonces has terminado con el problema. Si aún no está allí, convierta otra unidad usando el mismo método.

Una vez que se acostumbre a este método, puede escribir todas las conversiones en una línea. Por ejemplo, también podemos resolver nuestro problema de ejemplo de la siguiente manera:

/_Uds X /_millas X /_{60 minutos}

=/_Uds X /_millas X /_{60 minutos}

= 10 x 5280 pies x /_{60 minutos}

= 880 pies/min.

Método 3 de 3: hacer conversiones en el sistema métrico

1. Comprender el sistema métrico. El sistema métrico, también conocido como sistema decimal, está diseñado para facilitar la conversión. Para convertir de una unidad métrica a otra, todo lo que necesita hacer es trabajar con números redondos: 10, 100, 1000, etc.

2. Aprende los prefijos. Las unidades métricas de medida usan prefijos para mostrar qué tan grande o pequeña es la medida. Aquí hay un ejemplo con unidades de peso, pero todas las demás unidades métricas usan los mismos prefijos. Los prefijos a continuación son cursiva se muestra, pero la mayoría de las conversiones se pueden hacer solo con los más comunes, audaz prefijos.

kilogramos = 1000 gramos

hectogramos = 100 gramos

dekagramos = 10 gramos

gramo = 1 gramo

decidirgramo = 0,1 gramo (décimo)

centavosgramo = 0,01 gramo (centésimo)

miligramos = 0,001 gramos (milésimas)

3. Usa los prefijos en las conversiones. Si conoce los prefijos, no tiene que buscar la conversión cada vez que quiera convertir. Los prefijos ya indican la conversión. Aquí están algunos ejemplos:

Conversión de kilómetros a metros: kilo significa 1000, entonces 1 kilómetro = 1000 metros.

Convertir de gramo a miligramo: mili significa 0,001, por lo que 1 miligramo = 0,001 gramo.

4. Mover el punto decimal en lugar de hacer cálculos. Lo más útil de la conversión de métricas es que puede omitir todos los cálculos. Multiplicar por 10 es lo mismo que mover el decimal una posición a la derecha. Dividir un número por 10 es lo mismo que mover el punto decimal a la izquierda. Aquí hay un ejemplo:

Problema: convertir 65,24 kilogramos a gramos.

1 kilogramo = 1000 gramos. el numero de ceros es tres. Eso significa que multiplicamos por 10 tres veces, o simplemente movemos el punto decimal tres posiciones a la derecha.

65,24 x 10 = 652,4 (una vez multiplicado)

652,4 x 10 = 6524 (dos veces)

6524x10 = 65.240 (tres veces)

La respuesta es sesenta y cinco.240 gramos.

5. Practica los problemas más difíciles. Se vuelve un poco más complicado si las dos unidades que desea convertir tienen prefijos. La forma más fácil de resolver esto es convertir primero a la unidad base (sin prefijo), luego convertir a la unidad final. Aquí hay un ejemplo:

Problema: Convertir 793 mililitros a decalitros.

1 mililitro = 0,001 litro. Hay tres ceros, así que movemos el decimal tres lugares a la izquierda. (Recuerde, compartir es moverse hacia la izquierda.)

793 mililitros = 0,793 litros

10 litros = 1 decalitro, entonces 1 litro = 0,1 decalitro. Hay un cero, así que vamos a mover el punto decimal un lugar a la izquierda.

0,793 litros = 0.0793 calcomanía.

6. Comprueba tu respuesta. El error más fácil de cometer es multiplicar en lugar de dividir, o viceversa. Cuando obtenga su respuesta final, verifique si tiene sentido:

si vas a un mayor unidad, entonces el número menor. (Al igual que convertir 12 pulgadas a 1 pie).

si vas a un menor unidad, el número se convierte en más alto. (Al igual que convertir 1 pie a 12 pulgadas).

Si su resultado no coincide con este, verifique su trabajo nuevamente.

Consejos

Convertir recetas no siempre es fácil. Algunos países miden los ingredientes sólidos por peso (gramos) y otros por volumen (cucharillas, tazas). Busque en línea un convertidor para convertir un ingrediente específico usando su densidad.