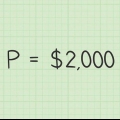El interés del año 1 será entonces de 60€ (1€.000x6%). Para calcular el interés del año 2, debe sumar el capital original al interés total hasta la fecha. En este caso, el principal del año 2 es igual a 1€.060 (1€.000 + 60€). El valor del bono es por lo tanto de 1€.060 y el interés a pagar se calcula en base a este valor. 
Multiplique el capital del año 2 por la tasa de interés del bono ($1.060 X 6% = 63,60 €). El interés obtenido es 3,60 € superior (63,60 € - 60,00 €). Eso es porque el capital ha aumentado de $1.000 a 1€.060. Para el año 3, el capital es de 1€.123,60 (1€.060 + 63,60 €). El interés del año 3 es de 67,42€. Ese importe se suma al principal para el cálculo del año 4. Cuanto más tiempo esté pendiente una deuda, mayor será el impacto del interés compuesto. Pendiente significa que la deuda aún debe ser pagada por el deudor. Sin interés compuesto, el interés devengado durante el año 2 sería de $60 (€1.000 X 6%). De hecho, cada año el interés sería de $60 si obtuvieras un interés compuesto. Esto se conoce como interés simple. 
Escriba los años (0-5) en las celdas A2 a A7. Escriba el director en la celda B2. Supongamos que empezaste con 1€.000. Tipo 1000. En la celda B3, escribe `= B2 *1,06` y presiona enter. Esto significa que su interés se capitaliza anualmente a una tasa del 6 % (0,06). Haga clic en la esquina inferior derecha de la celda B3 y arrastre la fórmula a la celda B7. Los números ahora se completan correctamente. Coloque un 0 en la celda C2. En la celda C3 escribe `=B3-B2` y presiona Enter. Esto da la diferencia entre los valores en las celdas B3 y B2, lo que representa el interés. Haga clic en la esquina inferior derecha de la celda C3 y arrastre la fórmula a la celda C7. Los valores deben ser llenados automáticamente. Repita este procedimiento durante tantos años como desee realizar un seguimiento. También puede cambiar fácilmente los valores del principal y la tasa de interés cambiando las fórmulas utilizadas y el contenido de las celdas. 

Determinar el monto principal de la inversión. Esta es la cantidad original de su inversión. Esto puede ser cuánto ha depositado en su cuenta o el precio original del bono. Por ejemplo, supongamos que su capital en una cuenta de inversión es de 5 €.000 es. Encuentre la tasa de interés de la inversión. La tasa de interés debe ser una cantidad anual, expresada como un porcentaje del monto principal. Por ejemplo, un tipo de interés del 3,45% sobre el principal de 5€.000. Al calcular, la tasa de interés debe ingresarse como un decimal. Conviértalo dividiendo la tasa de interés por 100. En este ejemplo se convierte en 3,45/100 = 0,0345. También necesita saber con qué frecuencia se capitaliza el interés. El interés generalmente se capitaliza anualmente, mensualmente o diariamente. Supongamos, por ejemplo, que se trata de intereses mensuales. Esto significa que su tasa de interés (`c`) debe ingresarse como 12. Determine sobre qué período desea calcular. Esto podría ser un objetivo anual de crecimiento, como 5 o 10 años, o el vencimiento del bono. La fecha de vencimiento de un bono es la fecha en que debe reembolsarse el principal de la inversión. Como ejemplo, estamos usando dos años aquí, así que ingrese un 2. 
El ejemplo de inversión entonces se ingresa de la siguiente manera: 
Calcular el exponente y la parte de la fórmula entre paréntesis por separado. Este es un concepto de las matemáticas llamado `orden de operaciones`. Puedes leer artículos sobre el orden de las operaciones en wikiHow. 
Primero calcula la fracción entre paréntesis. El resultado: 
Sumar números entre paréntesis juntos. El resultado: 
Resuelve la multiplicación dentro del exponente (la última parte arriba del paréntesis de cierre). El resultado debería verse así: 
Eleva el número entre paréntesis a la potencia del exponente. Esto se puede hacer en una calculadora ingresando primero el valor entre paréntesis (1.00288 en el ejemplo), presionando el botón  , y luego ingresando el exponente (24 en este caso), después de lo cual presiona Enter. El resultado de este ejemplo es
, y luego ingresando el exponente (24 en este caso), después de lo cual presiona Enter. El resultado de este ejemplo es  .
. Finalmente, multiplique el principal por el número entre paréntesis. El resultado en el ejemplo es 5€.000 x 1,0715 = 5 €.357.50. Este es el saldo de la cuenta al final del segundo año. 
Restar el principal de 5€.000 del valor futuro de 5€.357,50 y te llevas 5€.375,50 - 5 €.000 = 357,50 € Has ganado 357,50 € de intereses después de dos años. 

Asegúrese de convertir la tasa de interés anual a un número decimal. Lo haces dividiendo el porcentaje por 100. Por ejemplo, asumiendo la tasa de interés anterior de 3,45 %, dividimos 3,45 entre 100 y obtienes 0,0345. Para la frecuencia de interés, se utiliza el número de veces al año que se calcula el interés. Esto significa el número 1 anual, el 12 mensual y el 365 diario (no se preocupe por los años bisiestos). 
La fórmula final que utiliza esta información es la siguiente: 

Primero resuelve las fracciones dentro de los paréntesis. Esto significa dividir `i` por `c` en tres lugares, todo para el mismo resultado de 0.00288. Ahora la ecuación se ve así: 
Resuelve la suma entre paréntesis. Esto quiere decir que sumas el 1 al resultado de la parte anterior. Por lo tanto: 
Resolver la multiplicación dentro de los exponentes. Esto significa multiplicar los dos números que son más pequeños y están encima de los paréntesis de cierre. En el ejemplo: 2 x 12 = 24. Por lo tanto: 
Resuelve los exponentes. Esto significa aumentar la cantidad entre paréntesis con el resultado del último paso. En una calculadora, esto se hace ingresando el valor entre paréntesis (1.00288 en el ejemplo), presione  e ingrese el valor del exponente (24). Por lo tanto:
e ingrese el valor del exponente (24). Por lo tanto: 
sustraer. Resta 1 del resultado del último paso en la parte derecha de la ecuación (1.0715 - 1). Por lo tanto: 
Multiplicar. Esto significa multiplicar el capital por el valor entre paréntesis y la contribución mensual por el mismo valor entre paréntesis. Por lo tanto: 
dividir la fracción. Por lo tanto: 
Agregar. Finalmente, sume los dos números para obtener el valor futuro de la cuenta. Entonces: 5€.357,50 + 2 €.482,64 = 7 €.840.14. Este es el valor de la cuenta después de los dos años. 

Calcular interés compuesto
Contenido
El interés compuesto se diferencia del interés simple en que el rendimiento del interés se calcula tanto sobre la inversión original (principal) como sobre el interés acumulado hasta la fecha, en lugar de solo el principal. Por eso las cuentas de interés compuesto crecen más rápido que las cuentas de interés simple. Además, el valor crecerá aún más rápido si el interés se capitaliza varias veces al año. El interés compuesto (también llamado interés) se puede encontrar con varios productos de inversión y también como interés en ciertos tipos de préstamos, como deudas de tarjetas de crédito. Con las ecuaciones correctas, calcular cuánto crecerá una cantidad a través del interés compuesto es muy simple.
Pasos
Parte 1 de 3: Cálculo del interés compuesto anual

1. Definir interés compuesto anual. La tasa de interés indicada en su folleto de inversión o acuerdo de préstamo es anual. Si toma un préstamo de automóvil con, por ejemplo, un interés del 6%, paga un interés del 6% por año. Un interés compuesto de fin de año es el cálculo de interés compuesto más fácil.
- El interés compuesto de una deuda se puede calcular anualmente, mensualmente o incluso diariamente.
- Cuanto más a menudo se capitalice su deuda, más rápido se acumularán sus intereses.
- Puede ver el interés compuesto desde el punto de vista de un inversionista o de un deudor. El interés compuesto calculado con frecuencia significa que los ingresos por intereses de los inversores crecerán a un ritmo más rápido. También significa que el deudor deberá más intereses sobre una deuda pendiente.
- Por ejemplo, el interés se puede calcular anualmente en una cuenta de ahorros, mientras que el interés en un préstamo rápido se puede calcular mensualmente o incluso semanalmente.

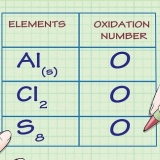
2. Calcule el interés anual compuesto para el año 1. Supongamos que posee un bono del gobierno de 1 €.000, a una tasa de interés del 6%. Los bonos del gobierno pagan dividendos cada año con base en el interés y el valor presente.

3. Calcular el interés compuesto para años posteriores. Para ver el mayor impacto del interés compuesto, calcule el interés para años posteriores. El principal sigue creciendo de año en año.

4. Crear un documento de Excel para calcular el interés compuesto. Puede ser útil visualizar el interés compuesto creando un modelo simple en Excel del crecimiento de su inversión. Comience abriendo un documento y etiquete la celda superior en las columnas A, B y C como "Año", "Valor" e "Interés ganado" respectivamente.
Parte 2 de 3: calcular el interés compuesto de las inversiones

1. Aprenda la fórmula de interés compuesto. La fórmula de interés compuesto calcula el valor futuro de la inversión después de un cierto número de años. La fórmula en sí es la siguiente:  Las variables dentro de la ecuación se definen de la siguiente manera:
Las variables dentro de la ecuación se definen de la siguiente manera:
 Las variables dentro de la ecuación se definen de la siguiente manera:
Las variables dentro de la ecuación se definen de la siguiente manera: - `FV` es el valor futuro. este es el resultado del calculo.
- `P` es su principal.
- `i` es la tasa de interés anual.
- `c` es la tasa de interés compuesto (con qué frecuencia se calcula el interés compuesto anualmente).
- `n` es el número de años a calcular.

2. Recoge las variables para la fórmula de interés compuesto. Si el interés se calcula con más frecuencia que anualmente, es difícil calcular la fórmula manualmente. Puede usar una fórmula de interés compuesto para cualquier cálculo. Para usar la fórmula, necesita la siguiente información:

3. Usa la fórmula. Sustituya sus variables en los lugares correctos. Verifique dos veces para asegurarse de que los ingresó correctamente. En particular, asegúrese de que el interés se ingrese en forma decimal y que haya utilizado el valor correcto para `c` (tasa de interés).


4. Completa los cálculos matemáticos en la fórmula. Simplifique el problema resolviendo primero los términos entre paréntesis, comenzando con la fracción.



 , y luego ingresando el exponente (24 en este caso), después de lo cual presiona Enter. El resultado de este ejemplo es
, y luego ingresando el exponente (24 en este caso), después de lo cual presiona Enter. El resultado de este ejemplo es  .
.
5. Resta el capital de tu respuesta. Esto devuelve la cantidad de interés.
Parte 3 de 3: calcular el interés compuesto con pagos regulares

1. Aprende la fórmula. Los cálculos de interés compuesto pueden crecer aún más rápido si realiza depósitos regulares, como transferir una cantidad mensual a una cuenta de ahorros. La fórmula es más larga que la utilizada para calcular el interés compuesto sin pagos regulares, pero sigue los mismos principios. La fórmula es la siguiente:  Las variables en la ecuación también son las mismas que en la ecuación anterior, con una adición:
Las variables en la ecuación también son las mismas que en la ecuación anterior, con una adición:
 Las variables en la ecuación también son las mismas que en la ecuación anterior, con una adición:
Las variables en la ecuación también son las mismas que en la ecuación anterior, con una adición: - `P` es el principal.
- `i` es la tasa de interés anual.
- `c` es la frecuencia de la tasa de interés y representa el número de veces que el interés se capitaliza anualmente.
- `n` es el número de años.
- `R` es el monto de la contribución mensual.

2. Completa las variables. Para calcular el valor futuro de este tipo de cuenta, necesita el capital (o valor actual) de la cuenta, la tasa de interés anual, la frecuencia de interés, la cantidad de años que se calculan y el monto de su contribución mensual. Esta información debe estar en su acuerdo de inversión.

3. Completa las variables. Seguimos con el ejemplo anterior: supongamos que decides transferir 100€ al mes a tu cuenta. Sobre esta cuenta, con un principal de 5€.000, el interés compuesto se calcula mensualmente con una tasa de interés anual de 3.45%. Vamos a calcular el crecimiento de la cuenta en dos años.


4. Resuelve la ecuación. De nuevo, no olvides el orden correcto de las operaciones. Esto significa que comienzas calculando los valores dentro de los paréntesis.



 e ingrese el valor del exponente (24). Por lo tanto:
e ingrese el valor del exponente (24). Por lo tanto: 




5. Restar el principal y los pagos. Para calcular el interés ganado, debe restar la cantidad que ha depositado. Esto significa sumar el principal, 5€.000, al valor total de las cantidades depositadas, así: 24 aportaciones (2 años x 12 meses/año) por los 100€ que has depositado cada mes, para un total de 2400€. El total es de 5€.000 + 2 €.400 = 7400€. Sorteo 7€.400 de descuento sobre el valor futuro de 7€.840,14, y te queda el importe de los intereses, 440,14€.

6. Amplíe su cálculo. Para ver realmente el beneficio del interés compuesto, imagine que sigue depositando dinero en la misma cuenta todos los meses durante 20 años (en lugar de dos). En este caso, el valor futuro se convierte en aproximadamente 45.000 dólares, aunque solo gastas 29€.000, lo que significa que tu interés devengado es de 16€.000 asciende a.
Consejos
- También puede calcular fácilmente el interés compuesto usando una calculadora de interés en línea. Puede encontrar un ejemplo en el sitio web del gobierno de los EE. UU.: https://www.inversor.gov/tools/calculators/compound-interest-calculator.
- Una forma rápida de determinar el interés compuesto es la `regla del 72`. Comience dividiendo 72 por la cantidad de interés que obtiene, digamos 4%. Entonces en este caso 72/4 = 18. Este resultado, 18, es aproximadamente el número de años que tardará en duplicar su inversión al tipo de interés actual. Tenga en cuenta que la regla 72 es solo una aproximación rápida, no un resultado exacto.
- También puede usar estos cálculos para hacer cálculos hipotéticos que le digan cuánto ganará según la tasa de interés, el capital, la tasa de interés o la cantidad de años.
Artículos sobre el tema. "Calcular interés compuesto"
Оцените, пожалуйста статью
Popular