Calcular interés

Contenido

Pasos

La mayoría de la gente conoce el concepto de interés, pero no todos saben cómo calcularlo. El interés es el valor agregado a un préstamo o anticipo para pagar el uso del dinero de otras personas durante un período de tiempo. El interés se puede calcular de tres maneras. El interés ordinario es el más fácil de calcular y generalmente se aplica a préstamos a corto plazo. El interés compuesto es un poco más complicado y vale más. Después de todo, el interés compuesto constante crecerá más rápido y esta es la fórmula que la mayoría de los bancos usan para los préstamos hipotecarios. La información que necesita para todos estos cálculos es generalmente la misma, pero las matemáticas son un poco diferentes para cada uno.

Pasos

Método 1 de 3: calcular el interés simple

1. Determinar el monto principal. El principal es la cantidad de dinero que utilizará para calcular el interés. Puede ser una cantidad que deposite en una cuenta de ahorros o ponga en algún tipo de inversión. En ese caso puedes calcular el interés que ganas. La alternativa es que si pide dinero prestado, como para una hipoteca, el principal es la cantidad que pide prestada y puede calcular el interés que debe.

En cualquier caso, ya sea que cobre o pague intereses, el monto del principal generalmente está simbolizado por la variable P.
Por ejemplo, si le pidió prestados $2,000 a un amigo, esos $2,000 son el capital.

2. Determinar el interés. Antes de que pueda calcular cuánto aumentará el valor del principal, necesita saber la tasa de interés a la que crecerá el principal. ese es tu interes. El interés generalmente se anuncia o se acuerda entre las partes antes de que se haga el préstamo.

Por ejemplo, suponga que le prestó dinero a un amigo bajo el acuerdo de que después de seis meses le devolverá los $2000 con un interés del 1,5 %. El interés único es del 1,5%. Pero antes de que pueda usar el porcentaje de 1.5%, debe convertirlo a un decimal. Para convertir porcentaje a decimal, divida el porcentaje por 100:

1,5% 100=0,015.

3. Consulta el plazo del préstamo. El término es otro nombre para la duración del préstamo. En algunos casos, usted acepta el plazo del préstamo al tomar prestada la cantidad. Por ejemplo: la mayoría de las hipotecas tienen un plazo fijo. En muchos casos, con un préstamo privado, el prestatario y el prestamista acordarán un plazo preestablecido.

Es importante que la duración del plazo corresponda a la tasa de interés, o al menos se mida en las mismas unidades. Por ejemplo: si se trata de una tasa de interés anual, entonces su plazo también debe medirse en años. Si la tasa se anuncia como del 3 % anual, pero el préstamo es solo por seis meses, entonces está calculando una tasa de interés anual del 3 % durante un período de 0,5 años.

Otro ejemplo: si la tasa pactada es del 1% mensual, y te prestas el dinero a seis meses, el plazo para el cálculo es de seis meses.

4. Calcular el interés. Para calcular el interés, multiplique el principal por la tasa de interés y el plazo del préstamo. Esta fórmula se puede expresar algebraicamente como:

I = pags * r * t

$I=P*r*t$

Usando el préstamo a un amigo ejemplo anterior, el principal (

pags

$pags$ ) igual a $2000 y el porcentaje (

r

$r$ ) es 0,015 durante un período de seis meses. Debido a que el contrato en este ejemplo fue por un plazo de seis meses, la variable

t

$t$ en este caso 1. Luego calcula el interés de la siguiente manera:

I = pags r t = (2000) (0, 015) (1) = 30

$I=Impre=(2000)(0.015)(1)=30$ . Por lo tanto, el interés adeudado es de 30 €.

Si desea calcular el monto total adeudado (A) con los intereses y el producto del principal, utilice la fórmula

a = pags (1 + r t)

$A=P(1+rt)$ . Este cálculo se ve así:

a = pags (1 + r t)

$A=P(1+rt)$

a = 2000 (1 + 0, 015 * 1)

$A=2000(1+0.015*1)$

a = 2000 (1, 015)

$A=2000(1.015)$

a = 2, 030

$= 2030$

5. Prueba con otro ejemplo. Digamos que deposita $5,000 en una cuenta de ahorros con un interés anual del 3%. Después de solo tres meses, retira el dinero, junto con cualquier interés.

a = pags (1 + r t)

$A=P(1+rt)$

a = 5000 (1 + 0, 03 * 0, 25)

$A=5000(1+0.03*0.25)$

a = 5000 (1, 0075)

$A=5000(1.0075)$

a = 5037, 5

$A=5037.5$

En tres meses ganarías 37,50 € de intereses.

Tenga en cuenta que t = 0,25, porque tres meses es un cuarto (0,25) del período original de un año.

Método 2 de 3: calcular el interés compuesto

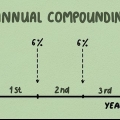
1. Entender qué es el interés compuesto. El interés compuesto significa que a medida que gana intereses, los intereses se agregan al monto de su cuenta y usted comienza a ganar (o pagar) intereses además de los intereses. Un ejemplo simple: si deposita $ 100 al 5% de interés anual, habrá ganado $ 5 de interés al final del año. Si vuelve a poner eso en su cuenta, al final del segundo año habrá ganado el 5% de $105, no solo los $100 originales. Con el tiempo, esto puede aumentar muy significativamente.

La fórmula para calcular el valor (A) del interés compuesto es la siguiente:

$a = pags (1 + \frac{r}{norte})^{norte t}$ $A=P(1+{frac{r}{n}})^{{nt}}$

2. Saber lo que significa el director. Al igual que con el interés simple, el cálculo comienza con el monto del capital. El cálculo es el mismo si va a calcular el interés sobre el dinero prestado o prestado. El principal es generalmente denotado por la variable

pags

$pags$ .

3. Determinar el porcentaje. La tasa de interés debe acordarse antes de que se preste el préstamo y mostrarse como un número decimal para el cálculo. Sepa que el porcentaje se puede convertir a un decimal dividiéndolo por 100 (o más rápido, moviendo el decimal dos posiciones a la izquierda). Asegúrese de saber para qué período se aplica la tasa de interés. El porcentaje tiene

r

$r$ como símbolo.

Por ejemplo, una compañía de tarjetas de crédito puede presentar su interés como 15% anual. Sin embargo, el interés generalmente se calcula mensualmente, por lo que probablemente desee saber cuál es la tasa de interés mensual. En ese caso, lo divides por 12 y obtienes un interés mensual de 1.25%. Estos dos porcentajes, 15% anual y 1,25% mensual, son iguales entre sí.

4. Sepa cuándo se capitaliza el interés. El interés compuesto significa que el interés se calcula periódicamente y se vuelve a sumar al monto principal. Para algunos préstamos, esto puede suceder una vez al año. Para otros, es cada mes o cada trimestre. Necesita saber con qué frecuencia se capitalizará el interés por año.

Si el interés se capitaliza anualmente, entonces n=1.

Si el interés se capitaliza trimestralmente, entonces el dinero n=4.

Imagen titulada Calcular interés Paso 10

5. Conoce el plazo del préstamo. El plazo es el período sobre el cual se calculará el interés. La duración se expresa generalmente en años. Si tiene que calcular el interés en un período diferente, debe convertirlo en años.

Por ejemplo: con un préstamo por un año,

t = 1

$t=1$ . No obstante, con un plazo de 18 meses,

t = 1, 5

$t=1,5$ .

Imagen titulada Calcular interés Paso 11

6. Determinar las variables de la situación. En este ejemplo, suponga que deposita $5,000 en una cuenta de ahorros con un interés mensual compuesto del 5%. ¿Cuál es el valor de esa cuenta después de tres años??

Primero determine qué variables necesita para resolver el problema. En este caso:

pags = 5000

$P=5000$

r = 0, 05

$r=0,05$

norte = 12

$n=12$

t = 3

$t=3$

Imagen titulada Calcular interés Paso 12

7. Aplicar la fórmula y calcular el interés compuesto. Una vez que comprenda qué debe hacerse y qué variables se necesitan, aplíquelas a la fórmula para calcular la tasa de interés.

En el problema anterior se ve así:

a = pags (1 + \frac{r}{norte})^{norte t}

$A=P(1+{frac{r}{n}})^{{nt}}$

a = 5000 (1 + 0, 05 12)^{12 * 3}

$A=5000(1+{frac{0.05}{12}})^{{12*3}}$

a = 5000 (1 + 0, 00417) 36

$A=5000(1+0.00417)^{{36}}$

a = 5000 (1, 00417) 36

$A=5000(1,00417)^{{36}}$

a = 5000 (1, 1616)

$A=5000(1,1616)$

a = 5808

$A=5808$

Entonces, después de tres años de interés compuesto, tiene una cantidad de 808 €, además de los 5000 € depositados originalmente.

Método 3 de 3: calcular el interés compuesto recurrente

Imagen titulada Calcular interés Paso 13

1. Entender qué es el interés compuesto revolvente. Como viste en el ejemplo anterior, el interés compuesto crece más rápido que el interés simple al agregar interés al principal en ciertos momentos. La compilación trimestral es más valiosa que la anual. La compilación mensual es incluso más valiosa que la anual. La situación más rentable sería cuando el interés se capitaliza constantemente, es decir, en cada momento. Tan pronto como se puede calcular el interés, se agrega a la cuenta y se agrega al principal. Esto es, por supuesto, sólo un caso teórico.

Utilizando un poco de matemáticas, los matemáticos han desarrollado una fórmula para simular el interés que se capitaliza continuamente y se agrega a la cuenta. Esta fórmula, utilizada para calcular el interés compuesto rotatorio, es:

$a = pags mi r t$ $A=Pe^{{rt}}$

Imagen titulada Calcular interés Paso 14

2. Conoce las Variables para el Cálculo de Intereses. La fórmula de interés compuesto rotativo es muy similar a las situaciones anteriores, pero con algunos ajustes menores. Las variables para la fórmula son:

a

$a$ es el valor futuro (o cantidad) de dinero que valdrá el préstamo después de capitalizar el interés.

pags

$pags$ es el director.

El constante

mi

$mi$ . Aunque parece una variable, en realidad es una constante. La carta

mi

$mi$ es un número especial llamado "constante de Euler", en honor al matemático Leonard Euler, quien descubrió sus propiedades.

La mayoría de las calculadoras gráficas avanzadas tienen un botón para

mi X

$e^{x}$ . Si pulsa este botón, con el número 1, así

mi 1

$e^{1}$ , entonces ves que el valor de

mi

$mi$ es aproximadamente 2.718.

r

$r$ es el interés por año.

t

$t$ es el plazo del préstamo, en años.

Imagen titulada Calcular interés Paso 15

3. Conoce los detalles de tu préstamo. Los bancos suelen utilizar intereses compuestos rotativos para las hipotecas. Supongamos que tienes 200€.000 quieren pedir prestado a un interés del 4,2% para una hipoteca de 30 años. Entonces, las variables que usará para este cálculo son:

pags = 200.000

$P = 200.000$

mi

$mi$ , de nuevo, no una variable sino la constante 2.718.

r = 0, 042

$r=0,042$

t = 30

$t=30$

Imagen titulada Calcular interés Paso 16

4. Usa la fórmula para calcular el interés. Aplica los valores a la fórmula para calcular la cantidad de intereses que tendrás que pagar por el préstamo a 30 años.