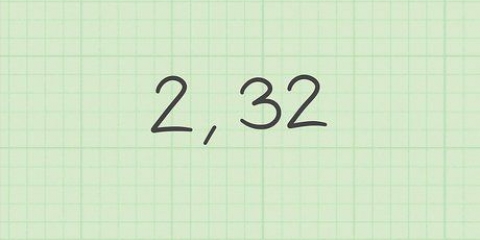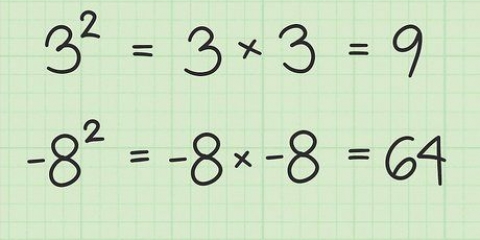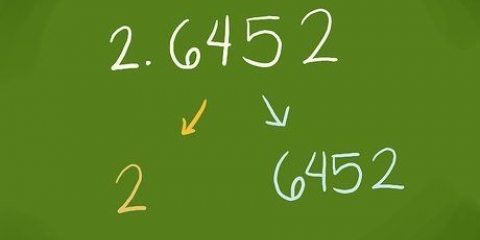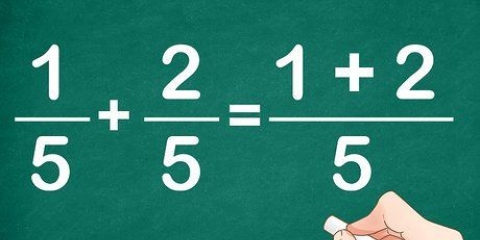Usar tablas logarítmicas

Contenido

Pasos
Consejos
Advertencias
Artículos de primera necesidad

Antes de la era de las computadoras y las calculadoras, las tablas se usaban para calcular rápidamente logaritmos, las tablas de logaritmos. Estas tablas aún pueden ser útiles para calcular o multiplicar logaritmos o números grandes rápidamente, una vez que descubras cómo usarlos.

Pasos

Método 1 de 3: leer una tabla de logaritmos

Imagen titulada Usar tablas logarítmicas Paso 6

1. Entender lo que es un logaritmo. 10 es 100. 10 es 1000. Las potencias 2 y 3 forman logaritmos con base 10, o también el logaritmo común de 100 y 1000. En general, un = c ser reescrito como Iniciar sesión_ac = segundo. Entonces "diez a la potencia de dos es 100" es el equivalente de "el logaritmo de 100 en base 10 es dos." Las tablas de registro tienen base 10 (use el registro regular), donde a por lo que siempre debe ser 10.

Multiplica dos números sumando sus potencias. Por ejemplo: 10 * 10 = 10, o 100 * 1000 = 100.000.
El logaritmo natural, sugerido por "en", es el logaritmo con base e, donde e es la constante 2.718. Este es un número útil para muchas áreas de las matemáticas y la física. Puede usar las tablas de logaritmo natural de la misma manera que las tablas de logaritmo normal, con base 10.

Imagen titulada Usar tablas logarítmicas Paso 7

2. Determina las características del número cuyo logaritmo natural quieres encontrar. 15 está entre 10 (10) y 100 (10), por lo que su logaritmo estará entre 1 y 2, si algo como 1 coma algo. 150 está entre 100 (10) y 1000 (10), por lo que su logaritmo estará entre 2 y 3, o algo así como 2 coma algo. La coma algo se llama demantisse; esto es lo que encontrarás en una tabla de registro. Lo que va antes de la coma (punto decimal) (1 en el primer ejemplo, 2 en el segundo) es el significativo.

Imagen titulada Usar tablas logarítmicas Paso 8

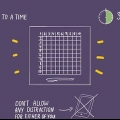
3. Deslice el dedo hacia abajo hasta la fila derecha de la tabla, a través de la columna en el extremo izquierdo. Esta columna mostrará los primeros dos o, para algunas tablas de registro grandes, tres dígitos del número del que está buscando el logaritmo de. Si busca el registro de 15.27 en una tabla de registro normal, vaya a la fila 15. Si busca el logaritmo de 2,57, vaya a la fila 25.

A veces, los números en esta fila tendrán un punto decimal, por lo que en realidad estás buscando 2.5 en lugar de 25. Puede ignorar este punto decimal ya que no afectará su respuesta.

Ignora también cualquier punto decimal en el número cuyo logaritmo quieras buscar, porque la mantisa para el logaritmo de 1,527 no es diferente de la de 152,7.

Imagen titulada Usar tablas logarítmicas Paso 9

4. En la fila correcta, desliza tu dedo sobre la columna correcta. Esta columna es la que está marcada con el siguiente dígito del número que está buscando el logaritmo de. Por ejemplo, si desea encontrar el registro de 15,27, su dedo estará en la fila 15. Deslice su dedo a lo largo de la fila hasta la columna 2. Ahora estás apuntando al número 1818. Escribe esto.

Imagen titulada Usar tablas logarítmicas Paso 10

5. La tabla de registro tiene una tabla de partes proporcionales. Deslice su dedo sobre la columna en esa tabla marcada con el siguiente dígito del número que está buscando. Para 15.27 esta cifra es 7. Su dedo está ahora en la fila 15 y la columna 2. Deslícese a la fila 15 y la columna de diferencias promedio, columna 7. Ahora estás señalando el número 20. Tenga en cuenta esto.

Imagen titulada Usar tablas logarítmicas Paso 11

6. Suma los números que encontraste en los dos pasos anteriores. Por 15.27 obtienes 1838. Esta es la mantisa del logaritmo de 15.27.

Imagen titulada Usar tablas logarítmicas Paso 12

7. Añadir el significativo. Dado que 15 está entre 10 y 100 (10 y 10), el logaritmo de 15 debe estar entre 1 y 2, por lo que 1.algo, entonces el significativo es 1. Combine el significativo con la mantisa para la respuesta final. Entonces el logaritmo de 15.27 es 1.1838.

Método 2 de 3: determinar el antilogaritmo

Imagen titulada Usar tablas logarítmicas Paso 13

1. Comprender la tabla antilogaritmo. Use esto cuando tenga el registro de un número, pero no el número en sí. En la fórmula 10 = x, n es el logaritmo en base común 10, o x. Si tiene x, puede encontrar n usando la tabla de registro. Si conoce n, determine x usando la tabla antilogaritmo.

El antilogaritmo también se conoce comúnmente como logaritmo inverso.

Imagen titulada Usar tablas logarítmicas Paso 14

2. Nótese lo significativo. Este es el número para el punto decimal. Si desea buscar el antilogaritmo de 2.8699, entonces el significativo es 2. En su mente, elimine esto del número que está buscando, pero escríbalo para que no lo olvide; será importante más adelante.

Imagen titulada Usar tablas logarítmicas Paso 15

3. Encuentra la fila correspondiente a la primera parte de la mantiss1. en 2.8699, la mantisa es 8699. La mayoría de las tablas antilogarítmicas, como la mayoría de las tablas de logaritmos, tienen dos números en la columna más a la izquierda, así que use su dedo para seguir la columna hacia abajo hasta llegar a 86.

Imagen titulada Usar tablas logarítmicas Paso 16

4. Deslice su dedo a la columna marcada con el siguiente número de la mantisa. Para 2.8699, deslice la fila marcada .86 para encontrar la intersección con la columna 9. Esto debería darte 7396. Tenga en cuenta esto.

Imagen titulada Usar tablas logarítmicas Paso 17

5. Si la tabla antilog también tiene una tabla de partes proporcionales, deslice su dedo a la columna en esa tabla marcada con el siguiente dígito de la mantisa. Asegúrate de que tu dedo permanezca en la misma fila. En este caso, mueva su dedo a la última columna de la tabla, la columna 9. La intersección de la fila 86 y la columna 9 con las diferencias de medias es 15. Tenga en cuenta esto.

Imagen titulada Usar tablas logarítmicas Paso 18

6. Sume los dos números de los dos pasos anteriores juntos. En nuestro ejemplo, estos son 7396 y 15. La suma de ambos es 7411.

Imagen titulada Usar tablas logarítmicas Paso 19

7. Usa el significativo para colocar el punto decimal. el significativo era 2. Esto significa que la respuesta debería estar entre 10 y 10, es decir, entre 100 y 1000. Para que el número 7411 esté entre 100 y 1000, el punto decimal debe colocarse después de tres dígitos para que el número sea aproximadamente 700, en lugar de 70, que es demasiado pequeño, o 7000, que es demasiado grande. Entonces la respuesta final es 741.1.

Método 3 de 3: multiplicar números usando tablas de registro

Imagen titulada Usar tablas logarítmicas Paso 20

1. Comprender cómo multiplicar números usando sus logaritmos. Sabemos que 10 * 100 = 1000. Escrito en potencias (o logaritmos), esto se convierte en 10 * 10 = 10. También sabemos que 1 + 2 = 3. En términos generales, 10 * 10 = 10. Entonces la suma de los logaritmos de dos números diferentes es el logaritmo del producto de estos números. Podemos multiplicar dos números con la misma base sumando sus potencias.

Imagen titulada Usar tablas logarítmicas Paso 21

2. Busca los logaritmos de los dos números que quieres multiplicar juntos. Utilice el método anterior para encontrar los logaritmos. Por ejemplo, si desea multiplicar 15,27 y 48,54, encontrará que el logaritmo de 15,27 es igual a 1,1838 y el logaritmo de 48,54 es 1,6861.

Imagen titulada Usar tablas logarítmicas Paso 22

3. Suma los dos logaritmos y has encontrado el logaritmo de la solución. En este ejemplo, sumas 1,1838 y 1,6861 y obtienes 2,8699. Este número es el logaritmo de tu respuesta.

Imagen titulada Usar tablas logarítmicas Paso 23

4. Busque el antilogaritmo del resultado del paso superior, para encontrar la solución. Haces esto encontrando el número en la tabla más cercano a la mantisa de este número (8699). Sin embargo, un método más eficiente y confiable es encontrar la respuesta en la tabla de antilogaritmos, como se describe en el método anterior. En este ejemplo obtienes 741.1.

Consejos

Siempre haga los cálculos en una hoja de papel y no de memoria, ya que estos son números largos y complicados, que pueden volverse bastante complicados.
Lee bien el título de la página. Un libro de logaritmos tiene unas 30 páginas y si usas la página equivocada, tu respuesta ya no será correcta.

Advertencias

Asegúrate de leer desde la misma fila. A veces es posible que se mezclen las filas y las columnas debido a los números pequeños y al breve interlineado.
La mayoría de las tablas solo tienen una precisión de 3 o 4 dígitos. Si encuentra el antilogaritmo de 2,8699 con una calculadora, la respuesta se redondeará a 741,2, pero la respuesta que obtiene con las tablas logarítmicas es 741,1. Esto se debe al redondeo de las tablas. Si necesita una respuesta más precisa, use una calculadora o algún otro método, en lugar de tablas de logaritmos.
Use los métodos descritos en este artículo para el logaritmo regular, o logaritmo en base 10, y asegúrese de que los números que busque también sean en base 10, también conocida como notación científica.