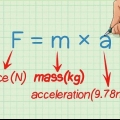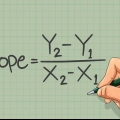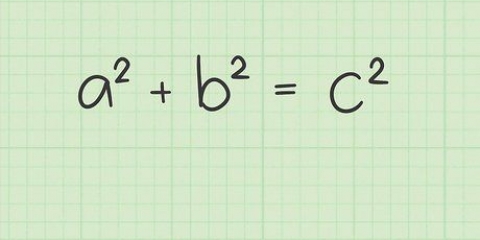Determinar la potencia neta: 9 pasos (con fotos)

Contenido

Pasos
- Parte 1 de 2: Determinación de la fuerza neta
- Parte 2 de 2: Cálculo de la fuerza diagonal

La fuerza neta es la cantidad total de fuerza que actúa sobre un objeto cuando se considera tanto su magnitud como su dirección. Un objeto con una fuerza neta de cero está estacionario. Una fuerza desequilibrada, o fuerza neta de magnitud mayor o menor que cero, da como resultado una aceleración del objeto. Una vez que tenga una potencia [[Power-calculate|calculado] o mide su tamaño, entonces es fácil combinarlos y encontrar la fuerza neta de esa manera. Delinear un diagrama de fuerza simple y asegurarse de que todas las fuerzas estén etiquetadas y en la dirección correcta hace que calcular la fuerza neta sea muy fácil.

Pasos

Parte 1 de 2: Determinación de la fuerza neta

1. Dibujar un diagrama de cuerpo libre. Un diagrama de cuerpo libre es un bosquejo rápido de un objeto que ilustra todas las fuerzas que actúan sobre el objeto y la dirección en la que actúan esas fuerzas. Lea el ejercicio y dibuje un contorno simple del objeto en cuestión y las flechas que muestran cualquier fuerza que actúe sobre ese objeto.

Por ejemplo: Calcule la fuerza neta de un objeto que pesa 20 N que se encuentra sobre una mesa y se empuja hacia la derecha con una fuerza de 5 N, pero se mantiene inmóvil por una fuerza de fricción de 5 N.

2. Determine las direcciones positiva y negativa de las fuerzas. De forma predeterminada, las flechas que apuntan hacia arriba o hacia la derecha son positivas y las flechas que apuntan hacia abajo o hacia la izquierda son negativas. Recuerda que puedes hacer que múltiples fuerzas actúen en la misma dirección. Las fuerzas opuestas siempre tendrán signos opuestos (uno positivo, uno negativo)..

Cuando trabaje con múltiples diagramas de potencia, asegúrese de mantener las instrucciones consistentes.

Etiquete la magnitud de cada fuerza con un signo `+` o `-` según la dirección de la flecha que indicó en el diagrama de fuerza.

Por ejemplo: la gravedad es una fuerza hacia abajo que la hace negativa. La fuerza normal es hacia arriba y por lo tanto positiva. La fuerza de empuje está a la derecha haciéndola positiva, mientras que la fuerza de fricción se opone a esta fuerza a la izquierda (negativa).

3. Etiquetar todos los poderes. Asegúrese de etiquetar todas las fuerzas que actúan sobre el objeto. Cuando un objeto descansa sobre una superficie, hay gravedad hacia abajo (F_gramo) y una fuerza igual en la dirección opuesta llamada fuerza normal (F_norte). Además de estas dos fuerzas, debes etiquetar el resto de las fuerzas mencionadas en el problema. Escriba la magnitud de cada fuerza en Newtons al lado de la etiqueta dada.

Una forma estándar de etiquetar las fuerzas es con una F mayúscula y la primera letra de la fuerza. Por ejemplo, si hay una fuerza debido a la fricción, la denotas con F_F.

Gravedad: F_gramo = -20N

Fuerza normal: F_norte = +20N

Fuerza de fricción: F_F = -5N

Fuerza de empuje: F_pags = +5N

4. suma todas las fuerzas. Ahora que ha indicado todas las fuerzas con dirección y magnitud, todo lo que tiene que hacer es sumarlas. Escribe una ecuación para la fuerza neta (F_sólo) donde F_sólo es la suma de todas las fuerzas que actúan sobre el objeto.

Por ejemplo: F_sólo = F_gramo + F_norte + F_F + F_pags = -20 + 20 -5 + 5 = 0 norte. Como la fuerza neta es 0 N, el objeto no se mueve.

Parte 2 de 2: Cálculo de la fuerza diagonal

1. Dibuja una tabla de fuerza. Cuando tienes una fuerza diagonal que actúa sobre el objeto en ángulo, debes ajustar la horizontal (F_X) y verticales (F_y) encontrar componentes de la fuerza para determinar su magnitud. Necesita trigonometría y el ángulo de dirección (generalmente θ `theta`) para esto. El ángulo de dirección θ siempre se mide en sentido antihorario desde el eje x positivo.

Dibujar el diagrama de fuerza incluyendo el ángulo de la fuerza diagonal.
Dibuja cada flecha en la dirección correcta en la que actúa la fuerza y márcala con el tamaño correcto.
Por ejemplo: Dibuje el diagrama de un objeto de 10 N con una fuerza de 25 N hacia arriba y hacia la derecha en un ángulo de 45°. También hay una fuerza de fricción a la izquierda de 10 N.
Los poderes incluyen: F_gramo = -10 N, F_norte = + 10 N, F_pags = 25 N, F_F = -10N.

2. Calcular F_X y F_y con ayuda detres razones trigonométricas. (SOS CAS TOA). Usando la fuerza diagonal (F) como la hipotenusa de un triángulo rectángulo y F_Xy como los catetos de ese triángulo, puedes calcular cualquier.

Recuerda: CAS es coseno (θ) = adyacente/hipotenusa. F_X = cos θ *F = cos(45°) *25 = 17,68 N.

Recuerda: SOS es seno(θ) = opuesto/hipotenusa. F_y = sen θ *F = sen(45°) *25 = 17,68 N.

Tenga en cuenta que múltiples fuerzas diagonales pueden actuar sobre un objeto simultáneamente, por lo que su F_X y F_y de cada fuerza en la tarea debe encontrar. Luego cuenta la F_X-agregue valores para la fuerza total en la dirección horizontal y agregue la F_y-valores para la fuerza total en la dirección vertical.

3. Editar el diagrama de potencia. Ahora que ha calculado las componentes horizontal y vertical separadas de la fuerza diagonal, puede dibujar un nuevo diagrama de fuerza que represente estas fuerzas. Borre la fuerza diagonal y en su lugar dibuje las flechas para los tamaños horizontal y vertical separados.

Por ejemplo, en lugar de una fuerza diagonal, el diagrama ahora tendrá una fuerza vertical apuntando hacia arriba con una magnitud de 17,68 N y una fuerza horizontal apuntando hacia la derecha con una magnitud de 17,68 N.

4. Sume todas las fuerzas en las direcciones x e y. Una vez que haya dibujado un nuevo diagrama de fuerza, calcule la fuerza neta (F_sólo) sumando todas las fuerzas horizontales y sumando todas las fuerzas verticales. Recuerde mantener todas las direcciones de los vectores consistentes a lo largo de la elaboración del problema.

Por ejemplo: Los vectores horizontales son todas las fuerzas a lo largo del eje x: F_netx = 17,68 - 10 = 7,68 N.

Los vectores verticales son todas las fuerzas a lo largo del eje y: F_nety = 17,68 + 10 - 10 = 17,68 norte.

5. Calcule la magnitud del vector de fuerza neta. En esta etapa tienes dos fuerzas: una en la dirección x y otra en la dirección y. La magnitud del vector fuerza es la hipotenusa del triángulo formado por estos dos vectores componentes. Solo usa el teorema de Pitágoras para calcular la hipotenusa: F_sólo = (F_netx + F_nety).

Por ejemplo: F_netx = 7,68 N y F_nety = 17,68 N

Usar en la ecuación: F_sólo = (F_netx + F_nety) = √ (7,68 + 17,68)

Resuelve: F_sólo = √ (7,68 + 17,68) = √(58,98 + 35,36) = √94,34 = 9,71 N.

La magnitud de la fuerza es de 9.71 N en una diagonal hacia arriba y hacia la derecha.