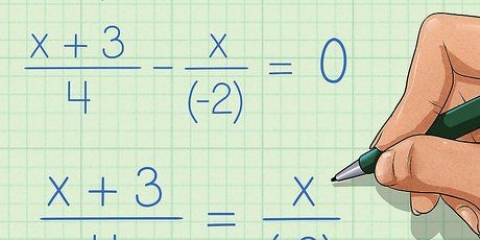Multiplicación cruzada: 8 pasos (con fotos)

Contenido

Pasos
- Método 1 de 2: multiplicación cruzada por una variable
- Método 2 de 2: Multiplicación cruzada con múltiples variables
Consejos

La multiplicación cruzada es una forma de resolver una ecuación, con una variable como parte de dos fracciones iguales entre sí. La variable es un número o cantidad desconocida, y la multiplicación cruzada hace que esta ecuación fraccionaria sea una ecuación simple, lo que le permite resolver la variable en cuestión. La multiplicación cruzada es especialmente útil cuando se trata de resolver una razón. Aquí está cómo hacer eso.

Pasos

Método 1 de 2: multiplicación cruzada por una variable

1. Multiplica el numerador de la fracción de la izquierda por el denominador de la fracción de la derecha. Digamos que estás trabajando en la ecuación 2/x = 10/13. Ahora multiplica 2 por 13. 2 x 13 = 26.

2. Multiplica el numerador de la fracción de la derecha por el denominador de la fracción de la izquierda. Multiplicar por 10. x * 10 = 10x. Puedes multiplicar en cruz en esta dirección primero; al final no importa, siempre y cuando multipliques ambos numeradores por los denominadores diagonales de la otra fracción.

3. Haz que los dos productos sean iguales. Haz que 26 sea igual a 10x. 26 = 10x. No importa qué número tomes primero; porque son equivalentes puedes moverlos de un lado a otro de la ecuación sin ninguna consecuencia; si tratas cada término como un todo.

Entonces, si tratas de resolver 2/x = 10/13 para x, obtienes 2 * 13 = x * 10, o 26 = 10x.

4. Resolver para la variable. Ahora que estás tratando con 26 = 10x, puedes comenzar a encontrar el denominador común dividiendo 26 y 10 por un número que tenga ambos denominadores divisibles por. Como ambos son números pares, es posible dividirlos por 2; 26/2 = 13 y 10/2 = 5. Ahora te queda 13 = 5x como ecuación. Luego, para aislar x, divide ambos lados de la ecuación por 5. Entonces 13/5 = 5/5, o 13/5 = x. Si desea que la respuesta sea una fracción decimal o un decimal, puede dividir ambos lados de la ecuación entre 10 para obtener 26/10 = 10/10, o 2.6 = x.

Método 2 de 2: Multiplicación cruzada con múltiples variables

1. Multiplica el numerador de la fracción de la izquierda por el denominador de la fracción de la derecha. Digamos que estás trabajando en la siguiente ecuación: (x + 3)/2 = (x + 1)/4. Multiplicar (x + 3) de 4 a 4(x+3) para obtener. esto se esta resolviendo 4x + 12.

2. Multiplica el numerador de la fracción de la derecha por el denominador de la fracción de la izquierda. Repita este procedimiento en el otro lado. (x+1) x2 = 2(x+1). Se convierte en 2(x +1) entonces 2x + 2.

3. Haga que los dos productos sean iguales y combine términos iguales. ahora tienes 4x + 12 = 2x + 2. Combina el X términos y las constantes en ambos lados de la ecuación.

Entonces, combina 4x y 2x por medio de 2x restar de ambos lados de la ecuación. Resuelto, esto produce la siguiente ecuación 2x + 12 = 2.

combinar ahora 12 y 2 por medio de 12 restar de ambos lados de la ecuación. Resuelto se ve así: 2x + 12-12 = 2-12.

Entonces la ecuación se convierte en: 2x = -10.

4. Resolver. Todo lo que tienes que hacer ahora es dividir ambos lados de la ecuación por 2. 2x/2 = -10/2 = x = -5. Después de multiplicar en cruz verás que x = -5. Puede regresar y verificar que todo esté correcto ingresando -5 para x para asegurarse de que ambos lados de la ecuación sean iguales. El resultado de esta comprobación es -1 = -1, y esto es cierto porque ambos lados de la ecuación son iguales. ¿El control, por ejemplo,. 0 = -1 volver la ecuación no es correcta, entonces algo salió mal.

Consejos

Tenga en cuenta que si ingresa otro número (por ejemplo, 5) en la misma ecuación, obtiene el siguiente resultado: 2/5 = 10/13. Incluso si vuelves a multiplicar el lado izquierdo de la ecuación por 5/5, obtienes 10/25 = 10/13, lo cual es claramente incorrecto. Este último caso muestra claramente que cometiste un error al multiplicar en cruz.