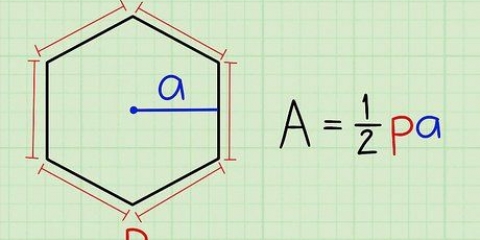
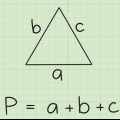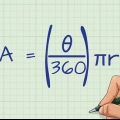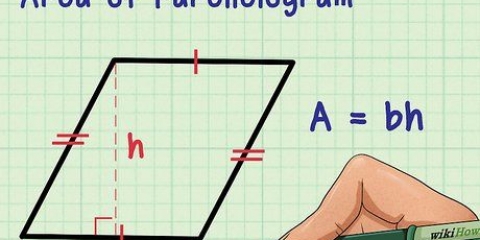Calcular ángulos: 8 pasos (con fotos)

Contenido

Pasos
- Método 1 de 2: calcular el ángulo en un polígono
- Método 2 de 2: calcular el ángulo en un triángulo rectángulo
Consejos
Artículos de primera necesidad

En geometría, un ángulo es el espacio entre dos semirrectas o segmentos de línea que tienen el mismo punto final o vértice. La forma más común de medir ángulos es en grados, donde un círculo completo son 360 grados. Puedes calcular el ángulo de un polígono si conoces la forma del polígono y el tamaño de los otros ángulos o, en el caso de un triángulo rectángulo, si conoces el tamaño de los dos lados.

Pasos

Método 1 de 2: calcular el ángulo en un polígono

1. Contar el número de lados del polígono.

2. Encuentra la suma de todos los ángulos en el polígono. La fórmula para encontrar la medida total de todos los ángulos interiores en un polígono es (norte – 2) x 180, donde norte es el número de lados, así como el número de ángulos del polígono. Algunos totales comunes de los ángulos en un polígono son:

Los ángulos en un triángulo (un polígono de 3 lados) suman 180 grados.

Los ángulos en un cuadrilátero (un polígono de 4 lados) suman 360 grados.

Los ángulos en un pentágono (un polígono de 5 lados) suman 540 grados.

Los ángulos en un hexágono (un polígono de 6 lados) suman 720 grados.

Los ángulos en un octágono (un polígono de 8 lados) suman 1080 grados.

3. Determinar si el polígono es un polígono regular. Un polígono regular es un polígono que tiene todos los lados de la misma longitud y todos los ángulos del mismo tamaño. Los triángulos y cuadrados equiláteros son ejemplos de polígonos regulares, mientras que el Pentágono en Washington DC es un ejemplo de un pentágono regular, y una señal de alto es un ejemplo de un octágono regular.

Si el polígono es un polígono regular, simplemente divida el total de todos los ángulos por el número de ángulos. Por lo tanto, cualquier ángulo en un triángulo equilátero es 180/3 = 60 grados, y cualquier ángulo de un cuadrado es 360/4 = 90 grados. (Aunque por definición un rectángulo no es un polígono regular, todos los ángulos también son rectos, y por lo tanto de 90 grados).

Si un polígono no es un polígono regular, necesitará saber la magnitud de los otros ángulos para calcular la magnitud del ángulo desconocido. Vaya al siguiente paso.

4. Sume los ángulos conocidos del polígono y reste el total del total de todas las medidas de los ángulos del polígono. La mayoría de los problemas de geometría similares funcionan con triángulos o cuadriláteros porque hay menos números para procesar, así que lo haremos.

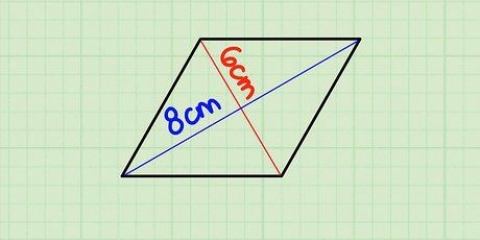
Si dos de los ángulos de un triángulo miden 60 y 80 grados, suma estos ángulos (60 + 80 = 140). Luego resta esta suma del total de los ángulos de un triángulo, 180 grados: 180-140=40 grados. (Tal triángulo, donde todos los ángulos son diferentes, se llama triángulo escaleno).

Puede escribir el método anterior como una fórmula: a=180 – (B + C), por lo que a es el ángulo que desea determinar, y B y C los ángulos que se conocen. Para polígonos con más de 3 lados, reemplace `180` con el total de los ángulos específicos de ese polígono y agregue un término diferente para cada ángulo conocido adicional.

Para algunos polígonos es posible una `solución más rápida` para determinar el ángulo desconocido. Un triángulo isósceles es un triángulo con dos lados de igual longitud y dos ángulos de igual magnitud. Un paralelogramo es un cuadrilátero con lados opuestos de igual longitud y ángulos diagonalmente opuestos de igual magnitud.

Método 2 de 2: calcular el ángulo en un triángulo rectángulo

1. Descubre lo que ya sabes. Un triángulo rectángulo se llama así porque uno de sus ángulos es un ángulo recto. Puedes determinar los otros ángulos si conoces alguno de los siguientes:

El tamaño del tercer ángulo. En este caso, puede sumar el tamaño del ángulo a 90, el número de grados del ángulo recto, luego restar el total de 180.
El tamaño de dos lados del triángulo. En este caso puedes determinar la magnitud del ángulo usando trigonometría.

2. Determinar qué función trigonométrica usar. Las funciones trigonométricas son cocientes entre dos de los tres lados de un triángulo. Aunque hay seis funciones trigonométricas, las tres siguientes son las más utilizadas:

Si conoces la longitud del lado opuesto (en relación con el ángulo) y la longitud de la hipotenusa (el lado opuesto al ángulo recto), usa la función seno (la longitud del lado opuesto dividida por la longitud de la hipotenusa). seda).

Si conoce la longitud del lado rectangular adyacente y la longitud de la hipotenusa, puede usar la función coseno (la longitud del lado adyacente dividida por la longitud de la hipotenusa).

Si conoce las longitudes de los lados opuestos y los lados adyacentes, puede usar la función tangente (la longitud del lado opuesto dividida por la longitud del lado adyacente).

3. Hallar la razón de los dos lados conocidos. Para los propósitos de este ejemplo, suponga que el lado opuesto al ángulo tiene una longitud de 5 y la hipotenusa tiene una longitud de 10. Dado que el opuesto y la hipotenusa están dados, la razón que tratamos aquí es la del seno.

Dividiendo el valor opuesto 5 por la hipotenusa (la hipotenusa) 10 da la fracción 5/10=0.5.

4. Encuentra el ángulo correspondiente a la razón de la función trigonométrica. Como estamos usando el seno para encontrar el ángulo, el ángulo que estamos buscando se llama arcoseno o seno inverso. Hay dos formas de encontrarlo:

En los días previos a las calculadoras, deberías consultar una tabla impresa de valores para el seno, el coseno y la tangente de los ángulos de 0 a 90 grados. Siga la columna del seno hasta que encuentre el valor `0.5` y luego encuentre el ángulo que corresponde a ese valor del seno.

Si tiene una calculadora con funciones trigonométricas, puede ingresar el seno como valor (si aún no ha usado la calculadora para dividir el lado opuesto por la hipotenusa para encontrar este valor) y luego presione la tecla o teclas apropiadas. Según la marca de la calculadora, presione una sola tecla con la etiqueta `sin` o una tecla con la etiqueta `Inv`, `2ndF` o `Shift` antes de presionar la tecla `sin`.

Sea cual sea el método que utilice para resolver este ejemplo, en todos los casos debe encontrar un ángulo de 30 grados.

Consejos

Los ángulos se denominan por el número de grados que miden. Como se mencionó anteriormente, un ángulo recto tiene 90 grados. Un ángulo mayor que 0 pero menor que 90 grados es un ángulo agudo. Un ángulo mayor de 90 pero menor de 180 grados es un ángulo obtuso. Un ángulo de 180 grados es un ángulo llano, mientras que un ángulo mayor de 180 grados es un ángulo de reentrada.
Dos ángulos con un total de 90 grados se llaman ángulos complementarios (Los dos ángulos que no sean el ángulo recto en un triángulo rectángulo son ángulos complementarios). Dos ángulos cuyos ángulos suman 180 grados se llaman ángulos suplementarios.