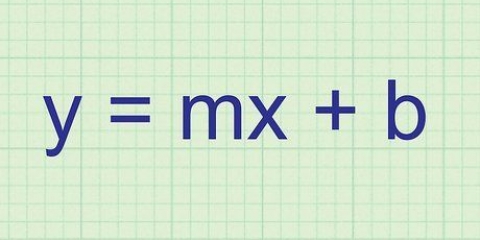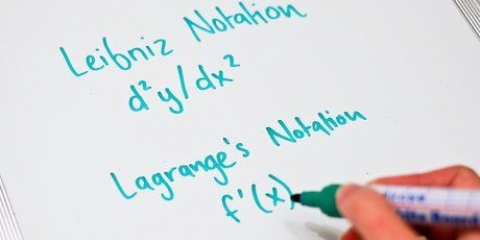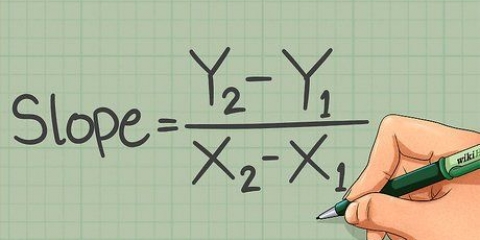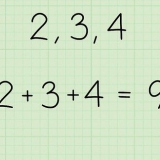Las funciones a menudo se escriben como  Esto significa que la función
Esto significa que la función  suma siempre 3 al número que tienes para
suma siempre 3 al número que tienes para  llenar. Si ingresas 2, anotas
llenar. Si ingresas 2, anotas  o
o 
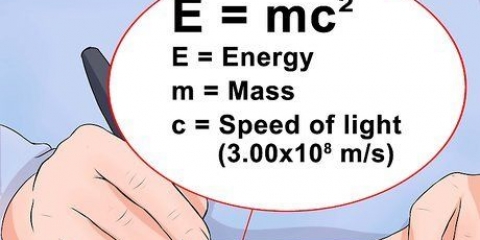
Las funciones también pueden mostrar movimientos complejos. La NASA, por ejemplo, tiene una función para describir la velocidad de un cohete, en función de la tasa de consumo de combustible, la resistencia del viento y el peso del cohete. 

Los límites son más fáciles de visualizar en un gráfico; por ejemplo, ¿hay puntos que están cerca de tocar un gráfico, pero nunca del todo?? Los límites pueden ser numéricos, infinitos o incluso inexistentes. Por ejemplo, con la secuencia de suma 1 + 2 + 2 + 2 + 2 + ... y esto continúa indefinidamente, entonces el número final se vuelve infinitamente grande. El límite entonces se vuelve infinito. 
Álgebra. Debes comprender los diferentes procesos y ser capaz de resolver ecuaciones y sistemas de ecuaciones con múltiples variables. Comprender los conceptos básicos de las colecciones. Practica haciendo gráficas. Geometría. La geometría es el estudio de las formas. Debe tener los conocimientos básicos de triángulos, rectángulos y círculos, y cómo calcular cosas como el perímetro y el área. Comprender ángulos, líneas y coordenadas trigonometría. La trigonometría es la rama de las matemáticas que se ocupa de las propiedades de los círculos y los triángulos rectángulos. Saber utilizar identidades trigonométricas, gráficas, funciones y funciones trigonométricas inversas. 
Muchos teléfonos inteligentes y tabletas hoy en día ofrecen aplicaciones gráficas económicas pero efectivas si no quiere o no puede comprar una calculadora gráfica. 

La aceleración es un derivado: te dice qué tan rápido algo está acelerando o desacelerando, es decir, cómo cambia su velocidad. 
La pendiente de la recta es el cambio en y dividido por el cambio en x`.` Cuanto mayor es la pendiente, más inclinada es la línea. Las líneas escarpadas cambian, por lo tanto, representan un cambio rápido. Actualiza tus conocimientos sobre cómo determinar la pendiente de una línea si se ha hundido un poco. 
por ejemplo, en  puedes elegir dos puntos cualesquiera y calcular la pendiente. llevar
puedes elegir dos puntos cualesquiera y calcular la pendiente. llevar  y
y  La pendiente entre estos puntos es entonces igual a
La pendiente entre estos puntos es entonces igual a  Esto significa que el cambio entre
Esto significa que el cambio entre  y
y  es igual a 2.
es igual a 2. 
Por ejemplo, los científicos están investigando qué tan rápido se extinguen algunas especies para salvarlas. Sin embargo, mueren más animales en invierno que en verano, por lo que no es útil estudiar la tasa de cambio durante todo el año; es mejor determinar la tasa de cambio dentro de un período más pequeño, como del 1 de julio al 1 de agosto. 
Piensa en el ejemplo donde sigues dividiendo 1 por 2, y con eso 1/2, 1/4, 1/8, etc. obtiene. Así que al final te acercas a cero, y la respuesta es `casi cero`. Los puntos están tan cerca uno del otro que son `casi iguales`. Esta es la naturaleza de los derivados. 

Hay diferentes notaciones para derivadas. En el paso anterior, las derivadas se indicaron con un signo de intercalación: la derivada de  luego escríbelo como
luego escríbelo como  Esto se llama notación de Lagrange.
Esto se llama notación de Lagrange. Hay otra forma que se usa a menudo para escribir derivadas. En vez de con cuidado, notas  Recuerda que la función
Recuerda que la función  depende de la variable
depende de la variable  Entonces escribimos la derivada como
Entonces escribimos la derivada como  --- la derivada de
--- la derivada de  hasta
hasta Esto se llama notación de Leibniz.
Esto se llama notación de Leibniz. 
¿Qué tan rápido se mueve la canica?? ¿A qué velocidad cambia la posición (o derivada) de la canica en movimiento?? Llamamos a este derivado `velocidad`. Haz rodar la canica por una rampa y observa cómo cambia la velocidad. ¿Cuál es la tasa de cambio, o derivada, de la velocidad de la canica?? Esta derivada es lo que llamamos `aceleración`. Rueda la canica a lo largo de una pista ondulada, como una montaña rusa. ¿Cuánto gana la canica en velocidad cuando rueda hacia abajo y cuánto desacelera la canica cuesta arriba?? ¿Qué tan rápido va la canica exactamente cuando está a la mitad de la primera colina?? Esta es entonces la tasa de cambio instantánea, o la derivada, de esa canica en ese punto específico. 




Suponga que suma muchos segmentos pequeños debajo del gráfico y que el ancho de cada segmento casi cero es. 
el primer simbolo,  es el símbolo de integración (esto es en realidad una S estirada).
es el símbolo de integración (esto es en realidad una S estirada). La segunda parte,  es la función. Si está dentro de la integral, se llama de integral.
es la función. Si está dentro de la integral, se llama de integral. y finalmente el  al final, que te dice qué variable estás integrando y a qué. Porque la función
al final, que te dice qué variable estás integrando y a qué. Porque la función  Dependiendo de
Dependiendo de  es aquello hacia lo que te integras.
es aquello hacia lo que te integras. Recuerda que la variable que integras puede no ser siempre  será, así que ten cuidado con lo que escribes.
será, así que ten cuidado con lo que escribes. 
Integrar por sustitución. Cálculo de integrales indefinidas. Integrar compartiendo. 
Por ejemplo, recuerda que la derivada de la velocidad es la aceleración, por lo que puedes usar la velocidad para encontrar la aceleración. Pero si solo conoce la aceleración de algo (como objetos que caen debido a la gravedad), puede integrar para encontrar la velocidad nuevamente! 
Esto te permite determinar el volumen de cualquier sólido, siempre y cuando tengas una función que lo represente. Por ejemplo, puede crear una función que siga el fondo de un lago y luego usarla para determinar el volumen del lago o la cantidad de agua que contiene.
Entender el análisis
Contenido
El análisis (también llamado cálculo) es una rama de las matemáticas centrada en límites, funciones, derivadas, integrales y series infinitas. Este tema cubre gran parte de las matemáticas y es la base de muchas de las fórmulas y ecuaciones utilizadas en física y mecánica. Probablemente necesitará varios años de matemáticas en la escuela secundaria para comprender correctamente el análisis, pero este artículo lo ayudará a comenzar a reconocer los conceptos clave, así como a una mejor comprensión de la teoría.
Pasos
Parte 1 de 3: Los fundamentos del análisis

1. El análisis es el estudio de cómo cambian las cosas. El análisis es una rama de las matemáticas que examina números y gráficos, generalmente tomados de datos del mundo real, y explica cómo cambian. Si bien esto puede no parecer muy útil al principio, el análisis es una de las ramas de las matemáticas más utilizadas. Imagine tener las herramientas que pueden decirle qué tan rápido está creciendo su negocio en un momento dado, o para trazar el curso de una nave espacial, y qué tan rápido se está agotando el combustible. El análisis es una herramienta importante en ingeniería, economía, estadística, química y física, y ha contribuido a muchas invenciones y descubrimientos.

2. Las funciones son relaciones entre dos números y se usan para mapear relaciones. Son reglas para la relación entre números, y los matemáticos las usan para hacer gráficas. En una función, cada entrada tiene exactamente un resultado. Por ejemplo: en  devuelve cualquier valor de
devuelve cualquier valor de  un nuevo valor para
un nuevo valor para  En caso de que
En caso de que  entonces es
entonces es  En caso de que
En caso de que  , entonces
, entonces  El análisis siempre estudia las funciones y cómo cambian, usando estas funciones para mapear las relaciones.
El análisis siempre estudia las funciones y cómo cambian, usando estas funciones para mapear las relaciones.
 devuelve cualquier valor de
devuelve cualquier valor de  un nuevo valor para
un nuevo valor para  En caso de que
En caso de que  entonces es
entonces es  En caso de que
En caso de que  , entonces
, entonces  El análisis siempre estudia las funciones y cómo cambian, usando estas funciones para mapear las relaciones.
El análisis siempre estudia las funciones y cómo cambian, usando estas funciones para mapear las relaciones. Esto significa que la función
Esto significa que la función  suma siempre 3 al número que tienes para
suma siempre 3 al número que tienes para  llenar. Si ingresas 2, anotas
llenar. Si ingresas 2, anotas  o
o 

3. Piensa en el concepto de infinito. El infinito es la repetición continua de un proceso. No es un lugar específico (no puedes ir al infinito), sino el comportamiento de un número o ecuación, si se hace para siempre. Esto es importante para estudiar el cambio: es posible que desee saber qué tan rápido se mueve su automóvil en un momento dado, pero ¿a qué velocidad se mueve su automóvil durante el segundo actual?? milisegundo? nanosegundo? Puede encontrar fragmentos de tiempo infinitamente más pequeños para ser aún más precisos, y ahí es cuando entra en juego el análisis.

4. Comprender el concepto de límites. Un límite te dice lo que sucede cuando algo se acerca al infinito. Toma el número 1 y divídelo por 2. Sigue dividiendo por 2, una y otra vez. 1 se convierte en ½ y luego 1/4, 1/8, 1/16, 1/32, etc. Cada vez que el número se vuelve más y más pequeño, `más cerca` de cero. Pero donde se detiene? ¿Cuántas veces hay que dividir 1 entre 2 para obtener cero?? En lugar de responder a esta pregunta, en el análisis usted propone una límite En este caso, el límite es.

5. Repase los conceptos matemáticos esenciales de álgebra, trigonometría y los conceptos básicos de las matemáticas. El análisis se basa en gran parte de las matemáticas que ha aprendido antes. Estar bien versado en todos los temas hace que sea mucho más fácil aprender y comprender el análisis. Algunos temas para refrescar tus conocimientos son:

6. Consigue una calculadora gráfica. El análisis no es fácil de entender sin ver lo que estás haciendo. Las calculadoras gráficas hacen que las funciones sean visuales para que pueda comprender mejor con qué ecuaciones está tratando. A menudo, los límites también se muestran en la pantalla y las derivadas y funciones se calculan automáticamente.
Parte 2 de 3: entender las derivadas

1. El análisis se utiliza para estudiar el `cambio en un momento específico`. Saber por qué algo cambia en un momento exacto es el núcleo del análisis. Por ejemplo, el análisis le brinda no solo la velocidad de un automóvil, sino también cuánto cambia esa velocidad en un momento dado. Este es uno de los usos más simples del análisis, pero muy importante. Imagínese lo importante que es esa información para determinar la velocidad necesaria para llevar una nave espacial a la luna!
- Determinar el cambio en un momento dado tiene diferenciar. La diferenciación es la primera de las dos ramas principales del análisis.

2. Usar derivadas para entender cómo cambian las cosas en un momento dado. Un `derivado` es una palabra elegante para algo que a menudo pone nerviosos a los estudiantes. Sin embargo, el concepto en sí no es tan difícil de entender, solo significa "qué tan rápido cambia algo". Los derivados que más te encontrarás en el día a día tienen que ver con la velocidad. Sin embargo, normalmente no lo llamas `la derivada de la velocidad`, sino simplemente `aceleración`.

3. Saber que la tasa de cambio es igual a la pendiente entre dos puntos. Este es uno de los descubrimientos más importantes del análisis. La tasa de cambio entre dos puntos es igual a la pendiente de la línea entre esos dos puntos. Solo piensa en una línea simple, como la de la ecuación  La pendiente de la recta es 3, lo que significa que por cada nuevo valor de
La pendiente de la recta es 3, lo que significa que por cada nuevo valor de 
 cambia por 3. La pendiente es la misma que la tasa de cambio: una pendiente de tres significa que la línea cambia en 3 (se vuelve tres veces más grande) por cada cambio en
cambia por 3. La pendiente es la misma que la tasa de cambio: una pendiente de tres significa que la línea cambia en 3 (se vuelve tres veces más grande) por cada cambio en  Cuándo
Cuándo  Cuándo
Cuándo 
 La pendiente de la recta es 3, lo que significa que por cada nuevo valor de
La pendiente de la recta es 3, lo que significa que por cada nuevo valor de 
 cambia por 3. La pendiente es la misma que la tasa de cambio: una pendiente de tres significa que la línea cambia en 3 (se vuelve tres veces más grande) por cada cambio en
cambia por 3. La pendiente es la misma que la tasa de cambio: una pendiente de tres significa que la línea cambia en 3 (se vuelve tres veces más grande) por cada cambio en  Cuándo
Cuándo  Cuándo
Cuándo 

4. Sepa que puede determinar la pendiente de líneas curvas. Determinar la pendiente de una línea recta es relativamente simple: cuánto cambia  por cualquier valor de
por cualquier valor de  Pero ecuaciones complejas como
Pero ecuaciones complejas como  para una curva, son mucho más difíciles de determinar. Sin embargo, aún puede determinar la tasa de cambio entre dos puntos: simplemente dibuje una línea entre los dos puntos y calcule la pendiente.
para una curva, son mucho más difíciles de determinar. Sin embargo, aún puede determinar la tasa de cambio entre dos puntos: simplemente dibuje una línea entre los dos puntos y calcule la pendiente.
 por cualquier valor de
por cualquier valor de  Pero ecuaciones complejas como
Pero ecuaciones complejas como  para una curva, son mucho más difíciles de determinar. Sin embargo, aún puede determinar la tasa de cambio entre dos puntos: simplemente dibuje una línea entre los dos puntos y calcule la pendiente.
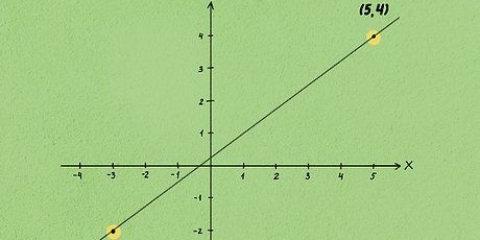
para una curva, son mucho más difíciles de determinar. Sin embargo, aún puede determinar la tasa de cambio entre dos puntos: simplemente dibuje una línea entre los dos puntos y calcule la pendiente. puedes elegir dos puntos cualesquiera y calcular la pendiente. llevar
puedes elegir dos puntos cualesquiera y calcular la pendiente. llevar  y
y  La pendiente entre estos puntos es entonces igual a
La pendiente entre estos puntos es entonces igual a  Esto significa que el cambio entre
Esto significa que el cambio entre  y
y  es igual a 2.
es igual a 2.
5. Si desea calcular el cambio con mayor precisión, asegúrese de que los puntos estén más juntos. Cuanto más cerca elija los dos puntos, más precisa será su respuesta. Suponga que desea saber cuánto acelera su automóvil cuando presiona el pedal del acelerador. No quieres medir el cambio de velocidad entre tu casa y el supermercado, sino el cambio de velocidad desde que pisas el acelerador. Cuanto más se acerque su lectura a esa fracción de segundo, más preciso será su cálculo del cambio.

6. Use líneas infinitamente cortas para determinar la `tasa de cambio instantánea`, o encuentre la derivada. Aquí es donde el análisis a menudo se vuelve un poco confuso, pero en realidad es el resultado de dos hechos simples. En primer lugar, sabes que la pendiente de una línea es igual a la rapidez con que cambia esa línea. En segundo lugar, sabe que cuanto más cerca estén los puntos de la línea entre sí, más precisa será la lectura. Pero, ¿cómo encuentra la tasa de cambio en un punto dado si la pendiente es la relación entre dos puntos?? La respuesta: Eliges dos puntos que están infinitamente cerca uno del otro.

7. Aprende a determinar varias derivadas. Hay muchas técnicas diferentes para encontrar una derivada dependiendo de la ecuación, pero la mayoría de ellas tienen sentido una vez que recuerdas los conceptos básicos de las derivadas anteriores. Todas las derivadas son una forma de encontrar la pendiente de una línea `infinitamente pequeña`. Ahora que sabe más sobre la teoría de la derivada, gran parte del trabajo consiste en encontrar las respuestas.

8. Determinar las ecuaciones derivadas para predecir la tasa de cambio en cualquier momento. Es útil determinar la tasa de cambio en cualquier momento usando derivadas, pero la belleza del análisis es que puedes crear un nuevo modelo para cualquier función. el derivado de  por ejemplo, es
por ejemplo, es  Esto significa que puedes encontrar la derivada para cualquier punto en un gráfico
Esto significa que puedes encontrar la derivada para cualquier punto en un gráfico  sustituyendo en la derivada. En el punto
sustituyendo en la derivada. En el punto  por lo cual
por lo cual  es la derivada 4, porque
es la derivada 4, porque 
 por ejemplo, es
por ejemplo, es  Esto significa que puedes encontrar la derivada para cualquier punto en un gráfico
Esto significa que puedes encontrar la derivada para cualquier punto en un gráfico  sustituyendo en la derivada. En el punto
sustituyendo en la derivada. En el punto  por lo cual
por lo cual  es la derivada 4, porque
es la derivada 4, porque 
 luego escríbelo como
luego escríbelo como  Esto se llama notación de Lagrange.
Esto se llama notación de Lagrange. Recuerda que la función
Recuerda que la función  depende de la variable
depende de la variable  Entonces escribimos la derivada como
Entonces escribimos la derivada como  --- la derivada de
--- la derivada de  hasta
hasta Esto se llama notación de Leibniz.
Esto se llama notación de Leibniz.
9. Trate de recordar ejemplos prácticos de derivados, si le resulta difícil de entender. El ejemplo más simple se basa en la velocidad, que abarca muchos derivados diferentes con los que nos encontramos todos los días. No lo olvide: una derivada es una medida de la rapidez con que algo cambia. Piensa en un experimento simple. Haces rodar una canica sobre una mesa y mides qué distancia se mueve cada vez y qué tan rápido. Ahora imagina que la canica rodando sigue una línea en un gráfico: usas derivadas para medir los cambios instantáneos en cualquier momento en esa línea.
Parte 3 de 3: Comprender las integrales

1. Sepa que puede usar el análisis para encontrar áreas y volúmenes complejos. El análisis le permite medir formas complejas que de otro modo serían difíciles de medir. Considere, por ejemplo, la cuestión de querer saber cuánta agua hay en un lago largo de forma irregular: es imposible medir cada litro de agua individualmente o usar una regla para medir la forma del lago. Con el análisis, puede estudiar cómo cambian los bordes del lago y luego usar esa información para determinar cuánta agua contiene.
- La realización de modelos geométricos y el estudio de los volúmenes ha integrar. El cálculo integral es la segunda rama importante del análisis.

2. Saber que la integración es el área bajo un gráfico. La integración se usa para medir el espacio debajo de una línea, lo que le permite determinar el área de formas extrañas o irregulares. Toma la ecuación  Eso parece una `U` invertida. Puedes calcular cuánto espacio hay debajo de la U, usando cálculo integral. Quizás se pregunte cuál es el sentido de eso, pero piense en su uso en los procesos de fabricación: puede crear una función que parezca una pieza nueva y usar la aritmética integral para encontrar el área de esa pieza y para ayudarle a pedir la cantidad correcta de material.
Eso parece una `U` invertida. Puedes calcular cuánto espacio hay debajo de la U, usando cálculo integral. Quizás se pregunte cuál es el sentido de eso, pero piense en su uso en los procesos de fabricación: puede crear una función que parezca una pieza nueva y usar la aritmética integral para encontrar el área de esa pieza y para ayudarle a pedir la cantidad correcta de material.
 Eso parece una `U` invertida. Puedes calcular cuánto espacio hay debajo de la U, usando cálculo integral. Quizás se pregunte cuál es el sentido de eso, pero piense en su uso en los procesos de fabricación: puede crear una función que parezca una pieza nueva y usar la aritmética integral para encontrar el área de esa pieza y para ayudarle a pedir la cantidad correcta de material.
Eso parece una `U` invertida. Puedes calcular cuánto espacio hay debajo de la U, usando cálculo integral. Quizás se pregunte cuál es el sentido de eso, pero piense en su uso en los procesos de fabricación: puede crear una función que parezca una pieza nueva y usar la aritmética integral para encontrar el área de esa pieza y para ayudarle a pedir la cantidad correcta de material.
3. Saber seleccionar un área a integrar. No puedes simplemente integrar una función completa. Por ejemplo,  es una línea diagonal que continúa para siempre, y no puedes integrar todo, porque nunca se detendría. Al integrar funciones, debe elegir un área, como todos los puntos entre
es una línea diagonal que continúa para siempre, y no puedes integrar todo, porque nunca se detendría. Al integrar funciones, debe elegir un área, como todos los puntos entre y
y 
 es una línea diagonal que continúa para siempre, y no puedes integrar todo, porque nunca se detendría. Al integrar funciones, debe elegir un área, como todos los puntos entre
es una línea diagonal que continúa para siempre, y no puedes integrar todo, porque nunca se detendría. Al integrar funciones, debe elegir un área, como todos los puntos entre y
y 

4. ¿Cómo se calcula el área de un rectángulo?. Suponga que tiene una línea plana sobre un gráfico, como  Para encontrar el área debajo de él, encuentra el área de un rectángulo entre
Para encontrar el área debajo de él, encuentra el área de un rectángulo entre  y
y  Esto es fácil de medir, pero no funcionará con líneas onduladas porque no puede convertirlas fácilmente en rectángulos.
Esto es fácil de medir, pero no funcionará con líneas onduladas porque no puede convertirlas fácilmente en rectángulos.
 Para encontrar el área debajo de él, encuentra el área de un rectángulo entre
Para encontrar el área debajo de él, encuentra el área de un rectángulo entre  y
y  Esto es fácil de medir, pero no funcionará con líneas onduladas porque no puede convertirlas fácilmente en rectángulos.
Esto es fácil de medir, pero no funcionará con líneas onduladas porque no puede convertirlas fácilmente en rectángulos.
5. Sepa que en el cálculo integral se suman muchos rectángulos pequeños para encontrar el área de un área. Si amplías enormemente una curva, parece una línea recta. Ves esto todos los días: no puedes ver la curvatura de la Tierra porque estás muy cerca de la superficie de la Tierra. La integración crea un número infinito de pequeños rectángulos debajo de una curva que son tan pequeños que son básicamente planos, lo que le permite contarlos. Todos estos rectángulos sumados forman el área del área bajo una curva.

6. Saber leer y escribir integrales correctamente. Las integrales constan de 4 partes. Una integral típica se ve así:


 es el símbolo de integración (esto es en realidad una S estirada).
es el símbolo de integración (esto es en realidad una S estirada). es la función. Si está dentro de la integral, se llama de integral.
es la función. Si está dentro de la integral, se llama de integral. al final, que te dice qué variable estás integrando y a qué. Porque la función
al final, que te dice qué variable estás integrando y a qué. Porque la función  Dependiendo de
Dependiendo de  es aquello hacia lo que te integras.
es aquello hacia lo que te integras. será, así que ten cuidado con lo que escribes.
será, así que ten cuidado con lo que escribes.
7. Más información sobre cómo encontrar integrales. El cálculo integral viene en muchas formas, y tienes que aprender muchas fórmulas diferentes para integrar cada función. Sin embargo, todos siguen los principios descritos anteriormente: la integración es la suma de un número infinito de cosas.

8. Saber que la integración es lo contrario de la diferenciación, y viceversa. Esta es una regla empírica de análisis que es tan importante que se le ha dado su propio nombre: el Teorema Fundamental de la Cuenta Integral. Dado que la integración y la diferenciación están tan estrechamente relacionadas, se puede usar una combinación de las dos para medir la tasa de cambio, la aceleración, la velocidad, la ubicación, el movimiento, etc. para determinar, sin importar la información que tenga.

9. Sepa que la integración también le permite controlar el volumen de los objetos 3D. Girar una forma plana es una forma de crear sólidos 3D. Imagínese una moneda girando sobre la mesa: observe cómo la moneda parece tomar la forma de una esfera a medida que gira. Este concepto le permite determinar el volumen mediante un proceso conocido como `volumen por rotación`.
Consejos
- La práctica hace al maestro, así que haz los ejercicios de práctica en tu libro de texto, incluso los que tu maestro no haya especificado, y verifica tus respuestas para que comprendas mejor los conceptos.
- Si no puedes resolver algo, pregúntale a tu maestro.
Artículos sobre el tema. "Entender el análisis"
Оцените, пожалуйста статью
Popular