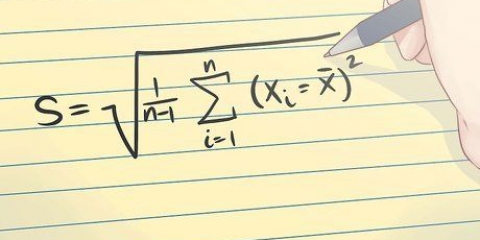Evaluación de la significación estadística: 15 pasos (con fotos)

Contenido

Pasos
Consejos
Advertencias

La prueba de hipótesis está respaldada por análisis estadístico. La significación estadística se calcula a partir de un valor p, que indica la probabilidad del resultado observado, dado que se cumple un teorema particular (la hipótesis nula). Si este valor p es menor que el nivel de significación establecido (generalmente 0.05), entonces el experimentador puede asumir que la hipótesis nula es falsa y aceptar la hipótesis alternativa. Usando una prueba t simple, puede calcular un valor p y comparar la importancia entre dos grupos diferentes de un conjunto de datos.

Pasos

Parte 1 de 3: Configuración de su experimento

Imagen titulada Evaluar la importancia estadística Paso 1

1. Define tu hipótesis. El primer paso para evaluar la significación estadística es definir la pregunta a responder y plantear su hipótesis. La hipótesis es una declaración sobre sus datos experimentales y las diferencias que pueden existir en la población. En todo experimento hay una hipótesis nula y otra alternativa. En general, comparará dos grupos para ver si son iguales o diferentes.

La hipótesis nula (H₀) generalmente establece que no hay diferencia entre sus dos conjuntos de datos. Por ejemplo: los alumnos que han leído el material antes de clase no obtienen mejores notas finales.
La hipótesis alternativa (H_a) es lo opuesto a la hipótesis nula y es la afirmación que intenta respaldar con sus datos experimentales. Por ejemplo: los estudiantes que han leído el material antes de clase obtienen mejores calificaciones finales.

Imagen titulada Evaluar la importancia estadística Paso 2

2. Establezca el nivel de importancia para determinar qué tan inusuales deben ser sus datos antes de que puedan considerarse significativos. El nivel de importancia (también llamado alfa) es el umbral que establece para determinar la importancia. Si el valor p es menor o igual al nivel de significación establecido, los datos pueden considerarse estadísticamente significativos.

Como regla general, el nivel de significación (o alfa) suele establecerse en 0,05, lo que significa que la probabilidad de observar accidentalmente las diferencias presentes en sus datos es solo del 5 %.

Un nivel de confianza más alto (y, por lo tanto, un valor de p más bajo) significa que los resultados son más significativos.

Si desea que los datos sean más confiables, establezca el valor p por debajo de 0.01. Los valores p más bajos se usan comúnmente en la industria al depurar productos. Es muy importante poder tener una gran confianza en que cada parte funciona exactamente como debe.

Para la mayoría de los experimentos hacia una hipótesis, un nivel de significancia de 0.05 es aceptable.

Imagen titulada Evaluar la importancia estadística Paso 3

3. Decidir usar una prueba de una cola o de dos colas. Una de las suposiciones que hace una prueba t es que los datos se distribuyen normalmente. Una distribución normal de datos forma una curva de campana con la mayoría de los datos de prueba en el medio. La prueba t es una prueba matemática para ver si los datos se encuentran fuera de la distribución normal (por encima o por debajo), en las "colas" de la curva.

Si no está seguro de si sus datos están por encima o por debajo del grupo de control, use una prueba doble. Le permite probar la importancia en ambas direcciones.

Si sabe en qué dirección tienden a moverse sus datos, use una prueba de una cola. En el ejemplo dado, espera que las calificaciones de los estudiantes mejoren; por eso usas una prueba de una cola.

Imagen titulada Evaluación de la importancia estadística Paso 4

4. Determinar el tamaño de la muestra con un análisis de fuerza. La potencia de una prueba es la probabilidad de que se observe el resultado esperado, dado un tamaño de muestra específico. El umbral común para la fuerza (o β) es 80%. Un análisis de potencia puede ser un poco complicado sin algunos datos preliminares porque necesita información sobre los valores medios esperados entre cada grupo y sus desviaciones estándar. Use una calculadora de análisis de fuerza en línea para determinar el tamaño de muestra óptimo para sus datos.

Los investigadores generalmente realizan un pequeño estudio piloto para informar su análisis de fortaleza y determinar el tamaño de muestra necesario para un estudio más grande y completo.

Si no tiene los recursos para hacer un estudio piloto complejo, haga algunas estimaciones de los promedios posibles basándose en la lectura de la literatura y los estudios que otras personas pueden haber realizado. Esto le dará un buen punto de partida para el tamaño de la muestra.

Parte 2 de 3: Cálculo de la desviación estándar

Imagen titulada Evaluar la importancia estadística Paso 5

1. Encuentre la fórmula para la desviación estándar. La desviación estándar es una medida de la dispersión de sus datos. Le brinda información sobre qué tan similar es cada punto de datos dentro de su muestra. A primera vista, la ecuación puede parecer un poco complicada, pero los siguientes pasos lo guiarán a través del cálculo. La fórmula es: s = √∑((x_I – µ)/(N – 1)).

s es la desviación estándar.
∑ indica que necesita sumar todos los valores de muestra recopilados.
X_I representa cada valor individual de sus datos.
µ es la media (o centro) de sus datos para cada grupo.
N es el total de la muestra.

Imagen titulada Evaluar la importancia estadística Paso 6

2. Promediar los datos de prueba en cada grupo. Para calcular la desviación estándar, primero debe promediar los datos de prueba en los grupos individuales. La media se denota con la letra griega mu o µ. Para hacer esto, sume cada dato y luego divídalo por el número total de datos.

Por ejemplo, para encontrar la calificación promedio del grupo que leyó el material antes de la clase, veamos algunos datos. Para simplificar, usamos un conjunto de datos de 5 puntos: 90, 91, 85, 83 y 94.

Sume todos los datos juntos: 90 + 91 + 85 + 83 + 94 = 443.

Divide la suma por el número de datos, N = 5:443 / 5 = 88,6.

La nota media de este grupo es de 88,6.

Imagen titulada Evaluación de la importancia estadística Paso 7

3. Restar cada métrica de la media. La siguiente parte del cálculo incluye la parte (x_I – µ) de la ecuación. Restas cada dato del promedio recién calculado. En nuestro ejemplo, terminas con cinco restas.

(90 – 88,6), (91–88,6), (85–88,6), (83–88,6) y (94–88,6).

Los números calculados ahora son 1.4, 2.4, -3.6, -5.6 y 5.4.

Imagen titulada Evaluación de la importancia estadística Paso 8

4. Eleva al cuadrado cada uno de estos números y súmalos. Cada uno de los nuevos números que acabas de calcular ahora se elevará al cuadrado. Este paso también crea signos negativos. Si tiene un signo menos después de este paso o al final de su cálculo, es posible que haya olvidado este paso.

En nuestro ejemplo ahora estamos trabajando con 1.96 5.76, 12.96, 31.36 y 29.16.

Sumando estos cuadrados da: 1,96 + 5,76 + 12,96 + 31,36 + 29,16 = 81,2.

Imagen titulada Evaluar la importancia estadística Paso 9

5. Divida esto por el tamaño de la muestra total, menos 1. La fórmula divide por N-1, porque corrige el hecho de que aún no ha contado una población completa; se toma una muestra de la población de todos los estudiantes para hacer una estimación.

Resta: N – 1 = 5 – 1 = 4

Parte: 81,2/4 = 20,3

Imagen titulada Evaluar la importancia estadística Paso 10

6. Saca la raíz cuadrada. Una vez que hayas dividido por el número de datos menos uno, calcula la raíz cuadrada de este último número. Este es el último paso para calcular la desviación estándar. Hay programas estadísticos que pueden hacer este cálculo por usted, después de ingresar los datos sin procesar.

En nuestro ejemplo, la desviación estándar de las calificaciones finales de los estudiantes que leyeron el material antes de la clase es: s = √20.3 = 4.51.

Parte 3 de 3: determinar la importancia

Imagen titulada Evaluar la importancia estadística Paso 11

1. Calcula la diferencia entre tus dos grupos de la muestra. Hasta este punto, el ejemplo solo ha cubierto uno de los grupos de muestra. Si desea comparar dos grupos, por supuesto tendrá datos de ambos grupos. Calcule la desviación estándar del segundo grupo de datos de prueba y utilícela para calcular la diferencia entre los dos grupos experimentales. La fórmula para la varianza es s_D = √((s₁/NORTE₁) + (s₂/NORTE₂)).

s_D es la varianza entre sus grupos.
s₁ es la desviación estándar del grupo 1, y N₁ es el tamaño de la muestra del grupo 1.
s₂ es la desviación estándar del grupo 2, y N₂ es el tamaño de la muestra del grupo 2.
Por el bien de nuestro ejemplo, digamos que los datos del Grupo 2 (estudiantes que no habían leído antes de clase) tenían un tamaño de muestra de 5 y una desviación estándar de 5.81. la varianza es:

s_D = √((s₁)/NORTE₁) + ((s₂)/NORTE₂))
s_D = √(((4.51)/5) + ((5.81)/5)) = √((20.34/5) + (33.76/5)) = √(4.07 + 6 .75) = √10.82 = 3.29.

Imagen titulada Evaluar la importancia estadística Paso 12

2. Calcule el t-score de sus datos. Con un puntaje t, puede convertir datos en un formulario que puede comparar con otros datos. Con las puntuaciones t, puede realizar una prueba t para calcular la probabilidad de que dos grupos difieran significativamente entre sí. La fórmula para una puntuación t es: t = (µ₁ – µ₂)/s_D.

µ₁ es el promedio del primer grupo.

µ₂ es la media del segundo grupo.

s_D es la varianza entre las muestras.

Utilice la media mayor como µ₁, entonces no tienes un valor negativo para t.

En nuestro ejemplo, digamos que la media de la muestra para el Grupo 2 (los que no leen) fue 80. El t-score es entonces: t = (µ₁ – µ₂)/s_D = (88,6 – 80)/3,29 = 2,61.

Imagen titulada Evaluación de la importancia estadística Paso 13

3. Determine el grado de libertad de su muestra. Cuando se usa el puntaje t, los grados de libertad se determinan usando el tamaño de la muestra. Sume el número de datos de prueba de cada grupo, luego divida por dos. En nuestro ejemplo, los grados de libertad; d.F.) 8, porque había cinco datos en el primer grupo y cinco en el segundo grupo ((5 + 5) – 2 = 8).

Imagen titulada Evaluar la importancia estadística Paso 14

4. Use una tabla t para evaluar la importancia. Se puede encontrar una tabla con puntuaciones t y el número de grados de libertad en un libro de estadísticas estándar o en línea. Mire la fila de grados de libertad para sus datos y encuentre el valor p que corresponde a su puntaje t.

con 8 días.F. y un puntaje t de 2.61, el valor p para una prueba de una cola se encuentra entre 0.01 y 0.025. Debido a que nuestro nivel de significancia establecido es menor o igual a 0.05, nuestros datos son estadísticamente significativos. Con estos datos, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa: Los estudiantes que leen el material antes de clase obtienen mejores calificaciones finales.

Imagen titulada Evaluar la importancia estadística Paso 15

5. Considere un estudio de seguimiento. Muchos investigadores realizan un pequeño estudio piloto con algunas mediciones para comprender cómo configurar un estudio más amplio. Otro estudio, con más mediciones, ayudará a aumentar su confianza en su conclusión.

Consejos

La estadística es un campo extenso y complicado. Tome una clase de educación secundaria o superior sobre inferencia estadística para comprender mejor la importancia estadística.

Advertencias

Este análisis es específico de una prueba t para probar las diferencias entre dos poblaciones normalmente distribuidas. Es posible que necesite una prueba estadística diferente según la complejidad de su recopilación de datos.